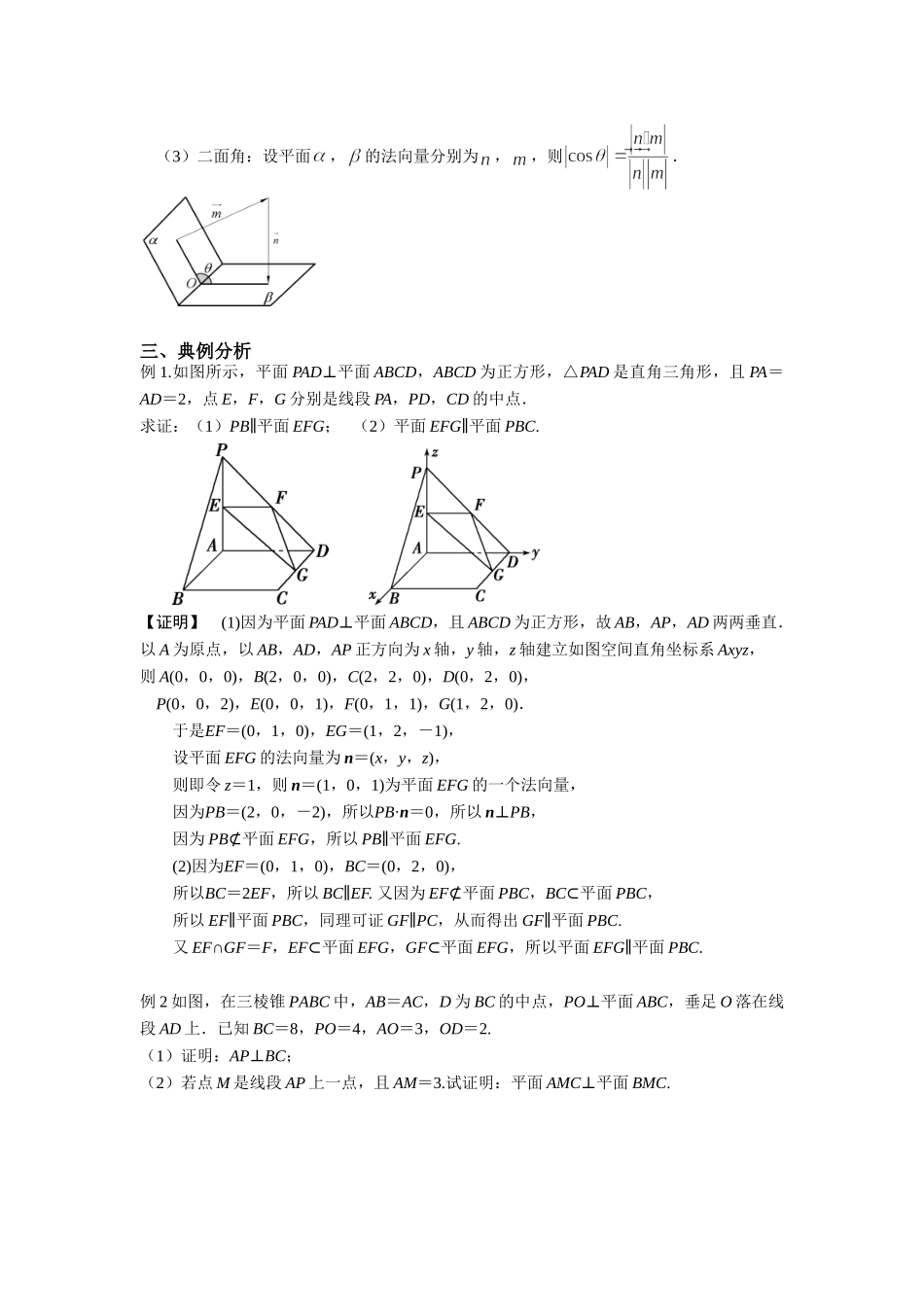
9.8空间向量在立体几何中的应用一、学习目标1.能用空间向量处理线面位置关系;2.能用空间向量求解空间角问题.二、知识回顾1.直线的方向向量与平面的法向量的确定(1)直线的方向向量:l是空间一直线,A,B是直线l上任意两点,则称AB为直线l的方向向量,与AB平行的非零向量也是直线l的方向向量.(2)平面的法向量①定义:与平面垂直的向量,称做平面的法向量.②确定:设a,b是平面α内两不共线向量,n为平面α的法向量,则求法向量的方程组为2.空间位置关系的向量表示位置关系向量表示直线l1,l2的方向向量分别为n1,n2l1∥l2n1∥n2⇔n1=λn2l1⊥l2n1⊥n2⇔n1·n2=0直线l的方向向量为n,平面α的法向量为ml∥αn⊥m⇔n·m=0l⊥αn∥m⇔n=λm平面α,β的法向量分别为n,mα∥βn∥m⇔n=λmα⊥βn⊥m⇔n·m=03.用向量求解空间角(1)异面直线所成角:设异面直线,的方向向量分别为,,则;(2)直线与平面所成角:设直线的方向向量为,平面的法向量为,则;(3)二面角:设平面,的法向量分别为,,则.三、典例分析例1.如图所示,平面PAD⊥平面ABCD,ABCD为正方形,△PAD是直角三角形,且PA=AD=2,点E,F,G分别是线段PA,PD,CD的中点.求证:(1)PB∥平面EFG;(2)平面EFG∥平面PBC.【证明】(1)因为平面PAD⊥平面ABCD,且ABCD为正方形,故AB,AP,AD两两垂直.以A为原点,以AB,AD,AP正方向为x轴,y轴,z轴建立如图空间直角坐标系Axyz,则A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),P(0,0,2),E(0,0,1),F(0,1,1),G(1,2,0).于是EF=(0,1,0),EG=(1,2,-1),设平面EFG的法向量为n=(x,y,z),则即令z=1,则n=(1,0,1)为平面EFG的一个法向量,因为PB=(2,0,-2),所以PB·n=0,所以n⊥PB,因为PB⊄平面EFG,所以PB∥平面EFG.(2)因为EF=(0,1,0),BC=(0,2,0),所以BC=2EF,所以BC∥EF.又因为EF⊄平面PBC,BC⊂平面PBC,所以EF∥平面PBC,同理可证GF∥PC,从而得出GF∥平面PBC.又EF∩GF=F,EF⊂平面EFG,GF⊂平面EFG,所以平面EFG∥平面PBC.例2如图,在三棱锥PABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上.已知BC=8,PO=4,AO=3,OD=2.(1)证明:AP⊥BC;(2)若点M是线段AP上一点,且AM=3.试证明:平面AMC⊥平面BMC.【证明】(1)如图所示,以O为坐标原点,以射线OD为y轴正半轴,射线OP为z轴正半轴建立空间直角坐标系Oxyz.则O(0,0,0),A(0,-3,0),B(4,2,0),C(-...