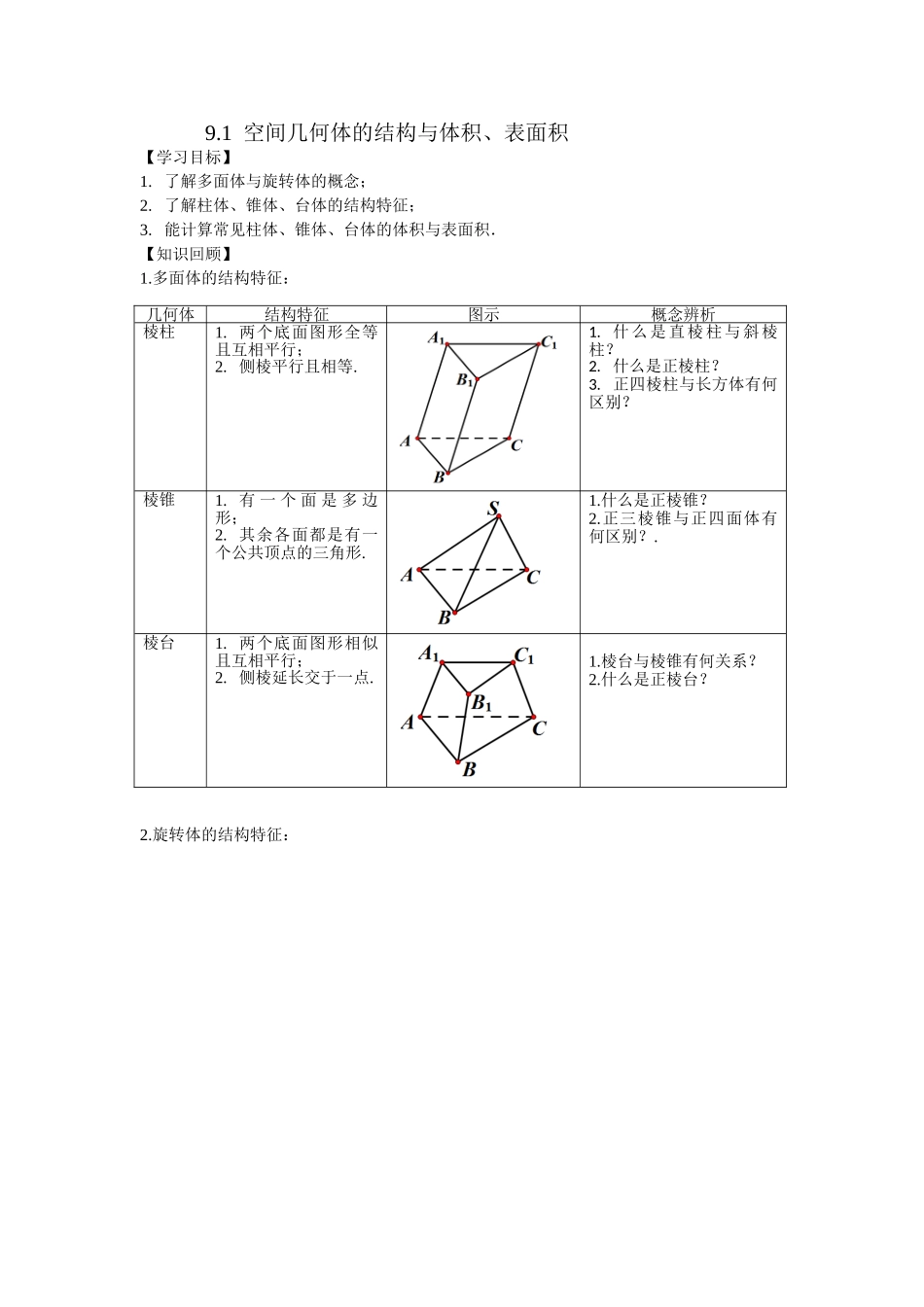
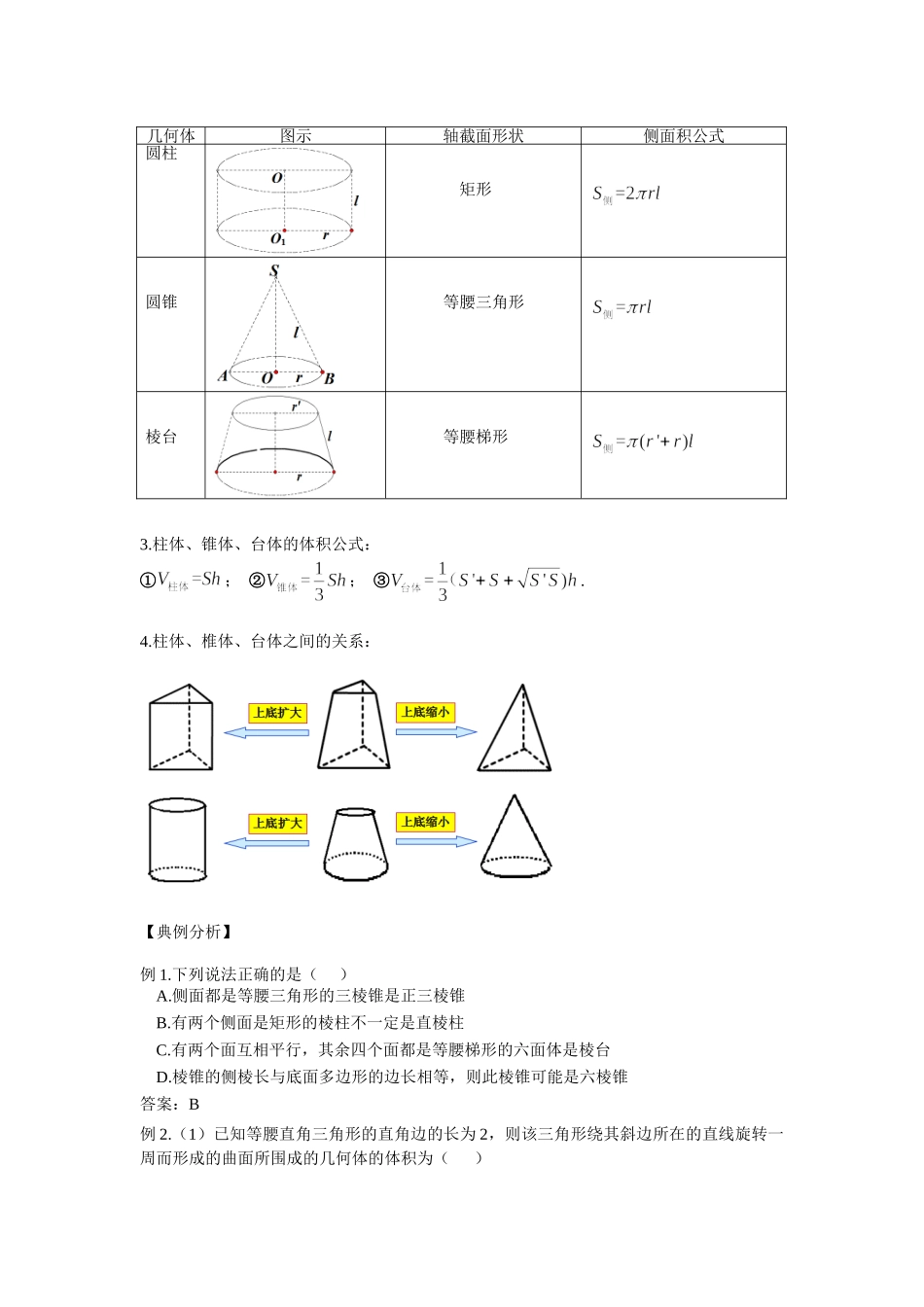
9.1空间几何体的结构与体积、表面积【学习目标】1.了解多面体与旋转体的概念;2.了解柱体、锥体、台体的结构特征;3.能计算常见柱体、锥体、台体的体积与表面积.【知识回顾】1.多面体的结构特征:2.旋转体的结构特征:几何体结构特征图示概念辨析棱柱1.两个底面图形全等且互相平行;2.侧棱平行且相等.1.什么是直棱柱与斜棱柱?2.什么是正棱柱?3.正四棱柱与长方体有何区别?棱锥1.有一个面是多边形;2.其余各面都是有一个公共顶点的三角形.1.什么是正棱锥?2.正三棱锥与正四面体有何区别?.棱台1.两个底面图形相似且互相平行;2.侧棱延长交于一点.1.棱台与棱锥有何关系?2.什么是正棱台?3.柱体、锥体、台体的体积公式:①;②;③.4.柱体、椎体、台体之间的关系:【典例分析】例1.下列说法正确的是()A.侧面都是等腰三角形的三棱锥是正三棱锥B.有两个侧面是矩形的棱柱不一定是直棱柱C.有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台D.棱锥的侧棱长与底面多边形的边长相等,则此棱锥可能是六棱锥答案:B例2.(1)已知等腰直角三角形的直角边的长为2,则该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为()几何体图示轴截面形状侧面积公式圆柱矩形圆锥等腰三角形棱台等腰梯形A.B.C.D.答案:B(2)已知一个圆锥的底面半径为6,其体积为,则该圆锥的侧面积为_________.答案:(3)圆台上、下底面面积分别是、,侧面积是,这个圆台的体积是________.答案:例3.(1)如图,正方体的棱长为1,、为线段、上的一点,则三棱锥的体积为________.答案:(2)如图,在三棱柱ABCCBA111中,FED,,分别是1,,AAACAB的中点,设三棱锥ADEF的体积为1V,三棱柱ABCCBA111的体积为2V,则21:VV________.答案:【课后作业】1.如图,长方体中被截去一部分,其中EH∥A′D′.剩下的几何体是()ABC1ADEF1B1CA.棱台B.四棱柱C.五棱柱D.六棱柱答案:C2.一个直角三角形的两条直角边长分别为1和2,将该三角形分别绕其两个直角边旋转得到的两个圆锥的体积之比为()A.1B.2C.4D.8答案:B3.如果底面直径和高相等的圆柱的侧面积是,那么圆柱的体积等于()A.B.C.D.答案:D4.已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长()A.B.C.D.答案:B5.埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与...