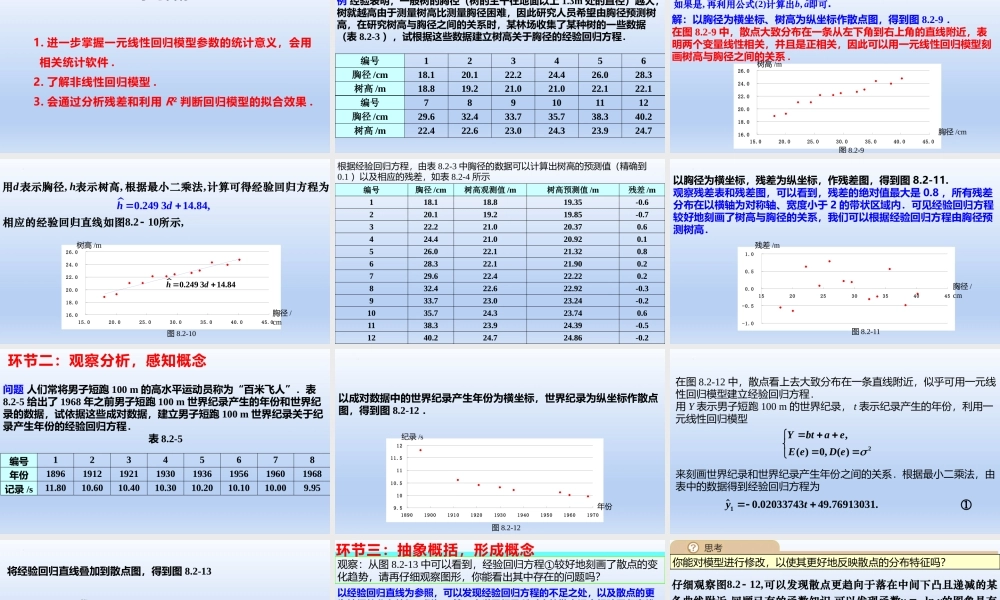
人教A版2019选择性必修第三册1.进一步掌握一元线性回归模型参数的统计意义,会用相关统计软件.2.了解非线性回归模型.3.会通过分析残差和利用R2判断回归模型的拟合效果.学习目标例经验表明,一般树的胸径(树的主干在地面以上1.3m处的直径)越大,树就越高由于测量树高比测量胸径困难,因此研究人员希望由胸径预测树高,在研究树高与胸径之间的关系时,某林场收集了某种树的一些数据(表8.2-3),试根据这些数据建立树高关于胸径的经验回归方程.编号123456胸径/cm18.120.122.224.426.028.3树高/m18.819.221.021.022.122.1编号789101112胸径/cm29.632.433.735.738.340.2树高/m22.422.623.024.323.924.7环节一:创设情境,引入课题16.018.020.022.024.026.015.020.025.030.035.040.045.0胸径/cm树高/m图8.2-9解:以胸径为横坐标、树高为纵坐标作散点图,得到图8.2-9.在图8.2-9中,散点大致分布在一条从左下角到右上角的直线附近,表明两个变量线性相关,并且是正相关,因此可以用一元线性回归模型刻画树高与胸径之间的关系.,,,ˆˆ,(2),ba分析:因为要由胸径预测树高所以要以成对样本数据的胸径为横坐标、树高为纵坐标描出散点进而得到散点图再根据散点图推断树高与胸径是否线性相关.如果是再利用公式计算出即可.16.018.020.022.024.026.015.020.025.030.035.040.045.0胸径/cm树高/m图8.2-100.249314.84hd0.249314.8,,,8.210,4,hddh用表示胸径表示树高根据最小二乘法计算可得经验回归方程为相应的经验回归直线如图所示根据经验回归方程,由表8.2-3中胸径的数据可以计算出树高的预测值(精确到0.1)以及相应的残差,如表8.2-4所示编号胸径/cm树高观测值/m树高预测值/m残差/m118.118.819.35-0.6220.119.219.85-0.7322.221.020.370.6424.421.020.920.1526.022.121.320.8628.322.121.900.2729.622.422.220.2832.422.622.92-0.3933.723.023.24-0.21035.724.323.740.61138.323.924.39-0.51240.224.724.86-0.2-1.0-0.50.00.51.015202530354045胸径/cm残差/m图8.2-11以胸径为横坐标,残差为纵坐标,作残差图,得到图8.2-11.观察残差表和残差图,可以看到,残差的绝对值最大是0.8,所有残差分布在以横轴为对称轴、宽度小于2的带状区域内.可见经验回归方程较好地刻画了树高与胸径的关系,我们可以根据经验回归方程由胸径预测树高.问题人们常将男子短跑100m的高水平运动员称为“百米飞人”.表8.2-5给出了1968年之前男子短跑100m世界纪录产生的...