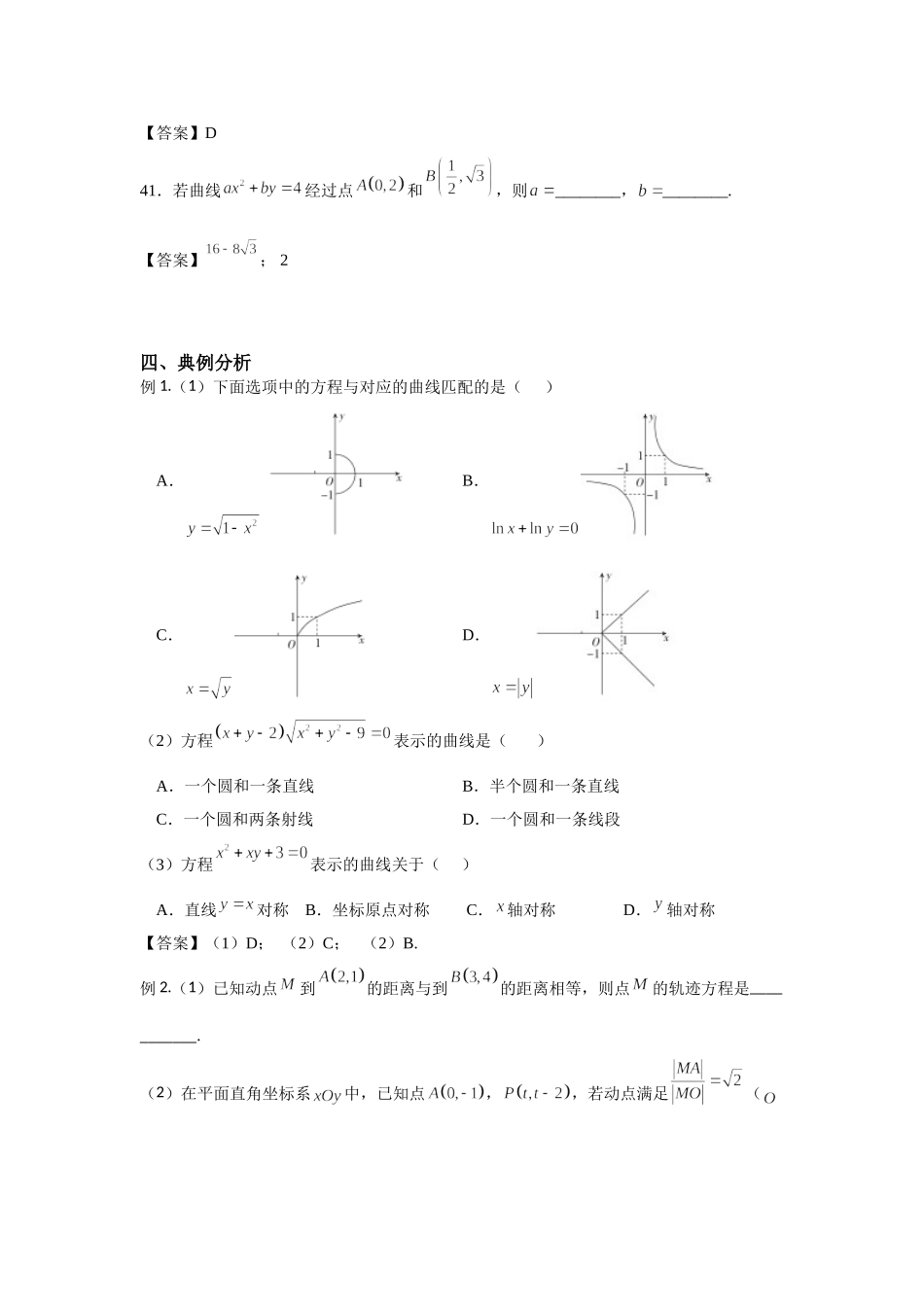
8.8曲线与方程一、学习目标1.理解曲线与方程的关系;2.掌握常见的求曲线方程(轨迹方程)的方法.二、知识要点1.曲线与方程:一般地,在直角坐标系中,如果某曲线C(看做动点的集合)上的点与一个二元方程的实数解建立了如下的关系:①曲线上点的坐标都是这个方程的解;②以这个方程的解为坐标的点都是曲线上的点.那么,这个方程叫做曲线的方程,这条曲线叫做方程的曲线.2.求动点的轨迹方程(曲线方程)的方法:(1)直接法;(2)转代法(相关点法);(3)定义法;(4)参数法;三、课前热身1.下列各点中,在曲线上的是()A.B.C.D.2.方程表示的曲线是()A.B.C.D.3.平面内已知点,若动点P满足,则点P的轨迹是()A.线段B.双曲线C.抛物线D.椭圆4.方程表示的曲线是()A.两条平行线B.一个直线和一条射线C.两条射线D.一条直线【答案】D41.若曲线经过点和,则________,________.【答案】;2四、典例分析例1.(1)下面选项中的方程与对应的曲线匹配的是()A.B.C.D.(2)方程表示的曲线是()A.一个圆和一条直线B.半个圆和一条直线C.一个圆和两条射线D.一个圆和一条线段(3)方程表示的曲线关于()A.直线对称B.坐标原点对称C.轴对称D.轴对称【答案】(1)D;(2)C;(2)B.例2.(1)已知动点到的距离与到的距离相等,则点的轨迹方程是___________.(2)在平面直角坐标系中,已知点,,若动点满足(为坐标原点),则的最小值是______.【答案】(1);(2).例3.(1)已知定点,点在圆上运动,则线段的中点的轨迹方程是()A.B.C.D.(2)设是椭圆上的动点,作轴,为垂足,则中点的轨迹方程为_________.(3)已知的两个顶点为,顶点C在曲线上运动,则的重心G的轨迹方程为______________.【答案】(1)C;(2);(3).例4.(1)已知圆过点且与直线相切,则圆心的轨迹方程为()A.B.C.D.(2)已知动点的坐标满足方程,则M的轨迹方程是()A.B.C.D.56.动圆M与圆外切,与圆内切,则动圆圆心M的轨迹方程是__________.【答案】(1)B;(2)D;(3).例5.已知圆上的一定点,点为圆内一点,,为圆上的动点.(1)求线段中点的轨迹方程;(2)若,求线段中点的轨迹方程.【答案】(1)解:设,则,设线段中点坐标为,则,解得,代入,得,即;(2)设线段中点坐标为,因为,所以,因为,所以,即,化简得.例6.(1)方程所表示的曲线为()A.双曲线B.椭圆C.双曲线的一部分D.椭圆的一部分(2)若直线与曲线...