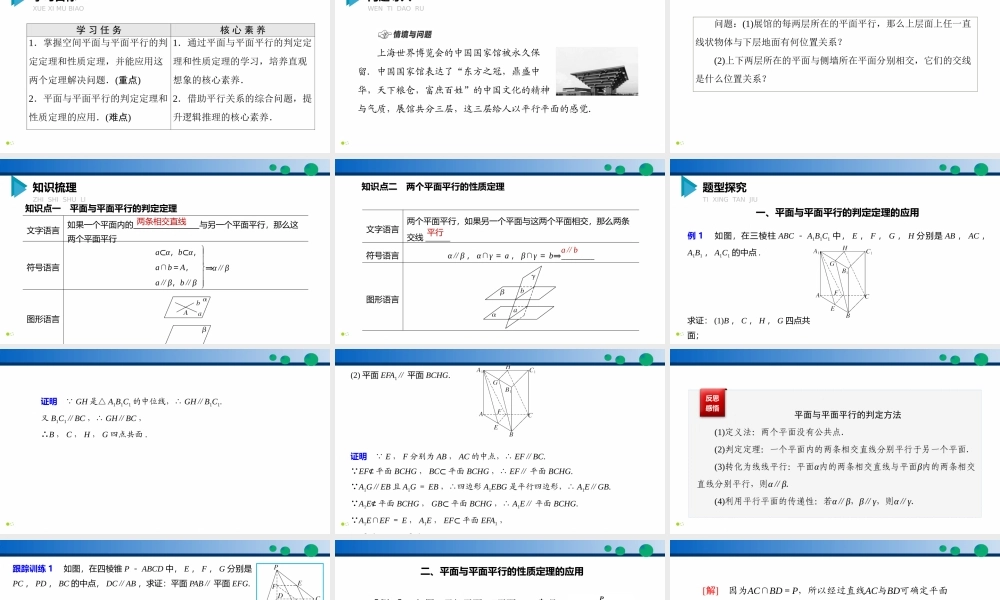
数学8.5.3平面与平面平行同步精品课件学习目标XUEXIMUBIAO学习任务核心素养1.掌握空间平面与平面平行的判定定理和性质定理,并能应用这两个定理解决问题.(重点)2.平面与平面平行的判定定理和性质定理的应用.(难点)1.通过平面与平面平行的判定定理和性质定理的学习,培养直观想象的核心素养.2.借助平行关系的综合问题,提升逻辑推理的核心素养.问题导入WENTIDAORU上海世界博览会的中国国家馆被永久保留.中国国家馆表达了“东方之冠,鼎盛中华,天下粮仓,富庶百姓”的中国文化的精神与气质,展馆共分三层,这三层给人以平行平面的感觉.问题:(1)展馆的每两层所在的平面平行,那么上层面上任一直线状物体与下层地面有何位置关系?(2)上下两层所在的平面与侧墙所在平面分别相交,它们的交线是什么位置关系?知识梳理ZHISHISHULI知识点一平面与平面平行的判定定理文字语言如果一个平面内的与另一个平面平行,那么这两个平面平行符号语言图形语言a⊂α,b⊂α,a∩b=A,a∥β,b∥β⇒α∥β两条相交直线知识点二两个平面平行的性质定理文字语言两个平面平行,如果另一个平面与这两个平面相交,那么两条交线______符号语言α∥β,α∩γ=a,β∩γ=b⇒________图形语言平行a∥b题型探究TIXINGTANJIU一、平面与平面平行的判定定理的应用例1如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点.求证:(1)B,C,H,G四点共面;证明 GH是△A1B1C1的中位线,∴GH∥B1C1.又B1C1∥BC,∴GH∥BC,∴B,C,H,G四点共面.(2)平面EFA1∥平面BCHG.证明 E,F分别为AB,AC的中点,∴EF∥BC. EF⊄平面BCHG,BC⊂平面BCHG,∴EF∥平面BCHG. A1G∥EB且A1G=EB,∴四边形A1EBG是平行四边形,∴A1E∥GB. A1E⊄平面BCHG,GB⊂平面BCHG,∴A1E∥平面BCHG. A1E∩EF=E,A1E,EF⊂平面EFA1,平平反思感悟平面与平面平行的判定方法(1)定义法:两个平面没有公共点.(2)判定定理:一个平面内的两条相交直线分别平行于另一个平面.(3)转化为线线平行:平面α内的两条相交直线与平面β内的两条相交直线分别平行,则α∥β.(4)利用平行平面的传递性:若α∥β,β∥γ,则α∥γ.跟踪训练1如图,在四棱锥P-ABCD中,E,F,G分别是PC,PD,BC的中点,DC∥AB,求证:平面PAB∥平面EFG.证明 E,G分别是PC,BC的中点,∴EG∥PB,又 EG⊄平面PAB,PB⊂平面PAB,∴EG∥平面PAB, E,F分别是PC,PD的中点,∴EF∥CD,又 AB∥CD...