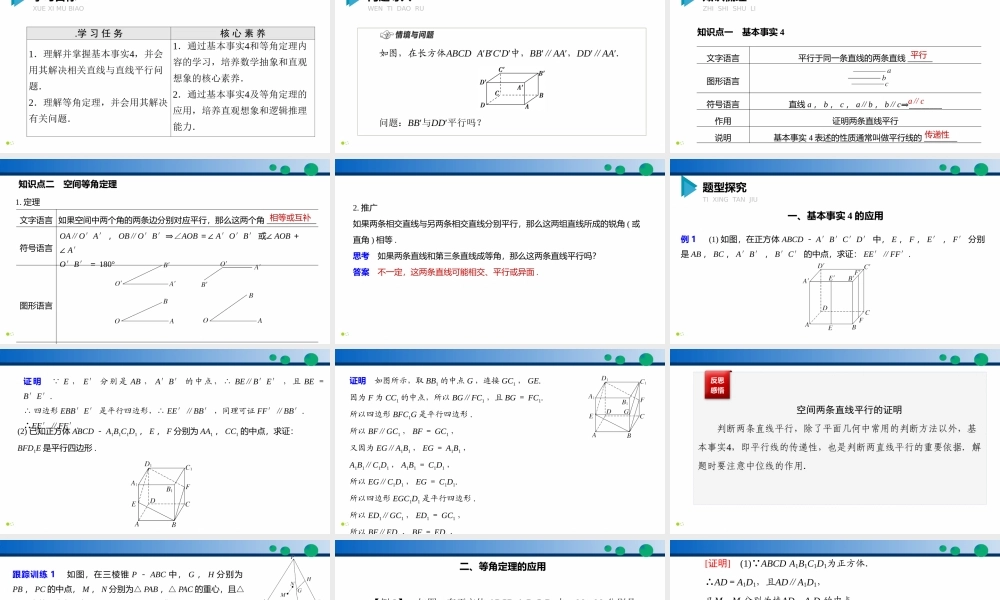
数学8.5.1直线与直线平行同步精品课件学习目标XUEXIMUBIAO.学习任务核心素养1.理解并掌握基本事实4,并会用其解决相关直线与直线平行问题.2.理解等角定理,并会用其解决有关问题.1.通过基本事实4和等角定理内容的学习,培养数学抽象和直观想象的核心素养.2.通过基本事实4及等角定理的应用,培养直观想象和逻辑推理能力.问题导入WENTIDAORU如图,在长方体ABCDA′B′C′D′中,BB′∥AA′,DD′∥AA′.问题:BB′与DD′平行吗?知识梳理ZHISHISHULI知识点一基本事实4文字语言平行于同一条直线的两条直线______图形语言符号语言直线a,b,c,a∥b,b∥c⇒________作用证明两条直线平行说明基本事实4表述的性质通常叫做平行线的________平行a∥c传递性知识点二空间等角定理1.定理文字语言如果空间中两个角的两条边分别对应平行,那么这两个角____________符号语言OA∥O′A′,OB∥O′B′⇒∠AOB=∠A′O′B′或∠AOB+∠A′O′B′=180°图形语言相等或互补2.推广如果两条相交直线与另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等.思考如果两条直线和第三条直线成等角,那么这两条直线平行吗?答案不一定,这两条直线可能相交、平行或异面.题型探究TIXINGTANJIU一、基本事实4的应用例1(1)如图,在正方体ABCD-A′B′C′D′中,E,F,E′,F′分别是AB,BC,A′B′,B′C′的中点,求证:EE′∥FF′.证明 E,E′分别是AB,A′B′的中点,∴BE∥B′E′,且BE=B′E′.∴四边形EBB′E′是平行四边形,∴EE′∥BB′,同理可证FF′∥BB′.∴EE′∥FF′.(2)已知正方体ABCD-A1B1C1D1,E,F分别为AA1,CC1的中点,求证:BFD1E是平行四边形.证明如图所示,取BB1的中点G,连接GC1,GE.因为F为CC1的中点,所以BG∥FC1,且BG=FC1.所以四边形BFC1G是平行四边形.所以BF∥GC1,BF=GC1,又因为EG∥A1B1,EG=A1B1,A1B1∥C1D1,A1B1=C1D1,所以EG∥C1D1,EG=C1D1.所以四边形EGC1D1是平行四边形.所以ED1∥GC1,ED1=GC1,所以BF∥ED,BF=ED,反思感悟空间两条直线平行的证明判断两条直线平行,除了平面几何中常用的判断方法以外,基本事实4,即平行线的传递性,也是判断两直线平行的重要依据.解题时要注意中位线的作用.跟踪训练1如图,在三棱锥P-ABC中,G,H分别为PB,PC的中点,M,N分别为△PAB,△PAC的重心,且△ABC为等腰直角三角形,∠ABC=90°,求证:GH∥MN.证明如图,取PA的中点Q,连接BQ,CQ,则M,N分别在BQ,CQ上. M,N...