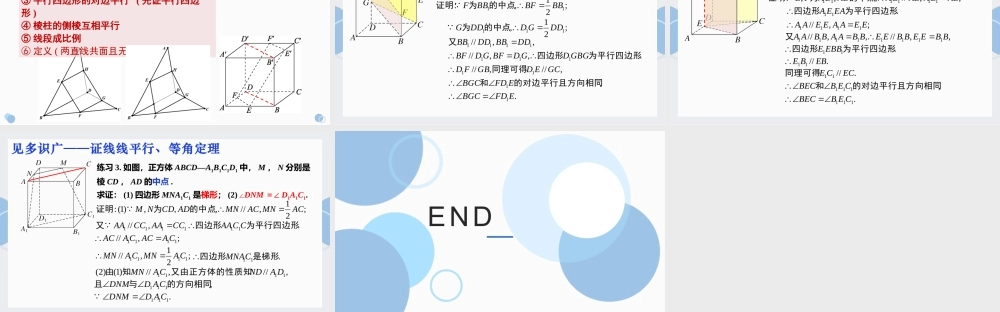
必修二《第八章立体几何初步》8.5.1直线与直线平行回顾与思考1.两直线平行的判定定理:内错角相等,两直线平行;同位角相等,两直线平行;同旁内角互补,两直线平行。平行于同一条直线的两直线平行;垂直于同一条直线的两直线平行。2.平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;两组对边分别平行的四边形是平行四边形。初中平面几何中高中立体几何中适用3.平行四边形的性质:平行四边形的对边平行且相等。证线线平行:①平行线的传递性ACBA′C′B′DD′长方体中, DC//AB,A′B′//AB,∴DC//A'B'.基本事实4.(空间中)平行于同一条直线的两条直线互相平行.①符号:若a//b,b//c,则a//c.②本质:平行线的传递性.③作用:证线线平行.④(区分)空间中垂直于同一条直线的两条直线__________________.平行或相交或异面长方体中,DC//AB,A′B′//AB,DC//A'B'吗?证线线平行:②三角形的中位线:(1),证明依题意得;21,//,BDFGBDFGBCDFG的中位线是;21,//,BDEHBDEHABDEH的中位线是.,//FGEHFGEH.是平行四边形四边形EHFG[例1]如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.(1)求证:四边形EFGH是平行四边形.(2)求证:EF//HG.(3)若AC=BD,则四边形EFGH是什么图形?(2)//.EFGHEFHG由四边形是平行四边形,可得,21,21,)3(ACEFBDEHEFGH中平行四边形.,EFEHACBD又菱形③平行四边形对边平行证线线平行的方法[例1]如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形.①平行线的传递性②三角形的中位线(找中点)③平行四边形的对边平行(先证平行四边形)④棱柱的侧棱互相平行BDFGBDFG21//BDEHBDEH21//FGEHFGEH且//EFGH平行四边形BDAC加ACEFBDEH2121菱形证线线平行:②三角形的中位线[变式]如图,正方体ABCD-A’B’C’D’中,E,F,E’,F’分别是AB,AD,B’C’,C’D’的中点,求证:四边形EFF’E’是平行四边形.③平行四边形对边平行,:依题意得证明;21,//,BDEFBDEFABDEF的中位线是;''21'',''//'','''''DBFEDBFEDBCFE的中位线是.''是平行四边形四边形BDBD,'','//',DDBBDDBB正方体中;'',//''BDDBBDDB;'',//''EFFEEFFE.''是平行四边形四边形FEFE④棱柱的侧棱互相平行等角定理及其运用P135定理.若空间中的两个角的两条边分别对应平行,则这两个角相等或互补.C'B'ABCA','//','//',',',',.3CCBBBBAACCBB...