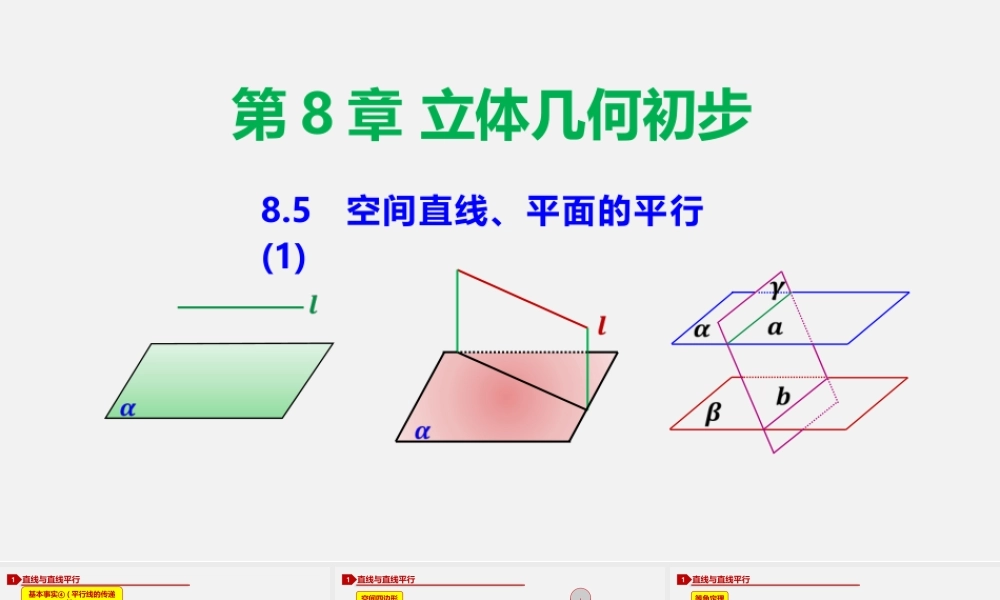
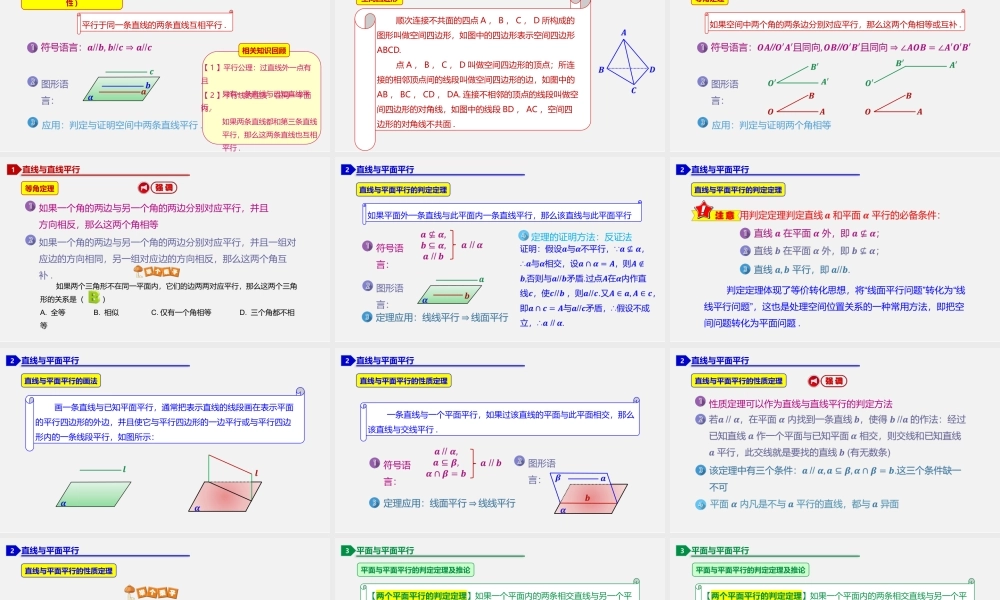
第8章立体几何初步8.5空间直线、平面的平行(1)直线与直线平行1平行于同一条直线的两条直线互相平行.基本事实④(平行线的传递性)图形语言:应用:判定与证明空间中两条直线平行.【1】平行公理:过直线外一点有且只有一条直线与已知直线平行.相关知识回顾【2】平行线的性质:在同一平面内,如果两条直线都和第三条直线平行,那么这两条直线也互相平行.直线与直线平行1顺次连接不共面的四点A,B,C,D所构成的图形叫做空间四边形,如图中的四边形表示空间四边形ABCD.点A,B,C,D叫做空间四边形的顶点;所连接的相邻顶点间的线段叫做空间四边形的边,如图中的AB,BC,CD,DA.连接不相邻的顶点的线段叫做空间四边形的对角线,如图中的线段BD,AC,空间四边形的对角线不共面.空间四边形直线与直线平行1如果空间中两个角的两条边分别对应平行,那么这两个角相等或互补.等角定理图形语言:应用:判定与证明两个角相等直线与直线平行1等角定理如果一个角的两边与另一个角的两边分别对应平行,并且一组对应边的方向相同,另一组对应边的方向相反,那么这两个角互补.如果一个角的两边与另一个角的两边分别对应平行,并且方向相反,那么这两个角相等如果两个三角形不在同一平面内,它们的边两两对应平行,那么这两个三角形的关系是()A.全等B.相似C.仅有一个角相等D.三个角都不相等直线与平面平行2直线与平面平行的判定定理如果平面外一条直线与此平面内一条直线平行,那么该直线与此平面平行图形语言:符号语言:定理的证明方法:反证法直线与平面平行2直线与平面平行的判定定理“”“判定定理体现了等价转化思想,将线面平行问题转化为线”线平行问题,这也是处理空间位置关系的一种常用方法,即把空间问题转化为平面问题.直线与平面平行2直线与平面平行的画法画一条直线与已知平面平行,通常把表示直线的线段画在表示平面的平行四边形的外边,并且使它与平行四边形的一边平行或与平行四边形内的一条线段平行,如图所示:直线与平面平行2直线与平面平行的性质定理一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么该直线与交线平行.图形语言:符号语言:直线与平面平行2直线与平面平行的性质定理性质定理可以作为直线与直线平行的判定方法直线与平面平行2直线与平面平行的性质定理平面与平面平行3平面与平面平行的判定定理及推论【两个平面平行的判定定理】如果一个平面内的两条相交直线与另一个平面平行,那么这两个平面平行.图形语言:符号...