8.3.3球的表面积和体积课件-2022-2023学年高一下学期数学人教A版（2019）必修第二册.pptxVIP免费

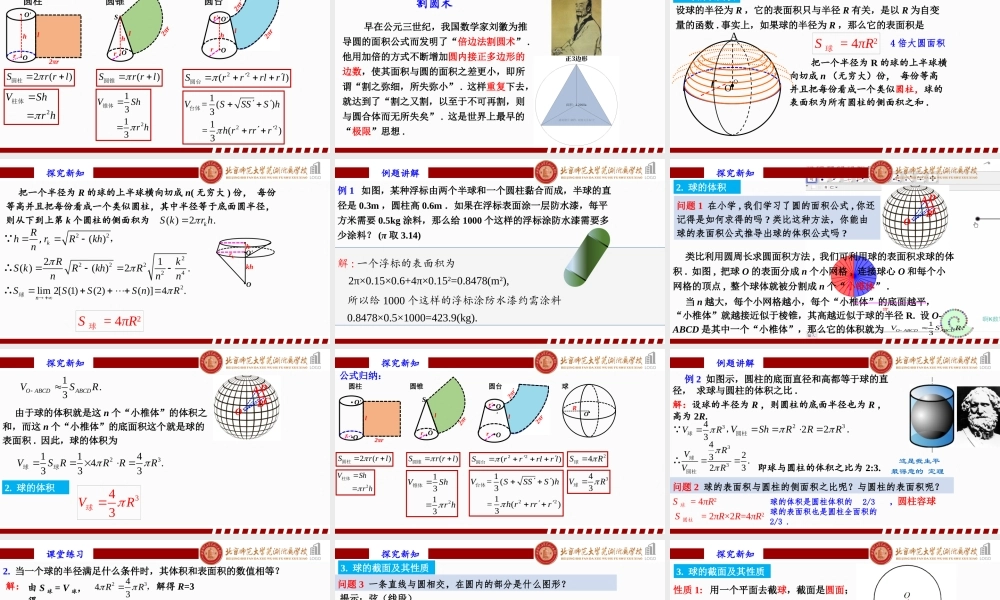
8.3.3球表面积和体积盛琪第八章立体几何初步01/26/2025LOGO引入2VShrh柱体21313VShrh锥体221=()31=()3VSSSShhrrrr台体圆柱圆锥圆台2()Srrl圆柱()Srrl圆锥22()Srrrlrl圆台lOO'2πrr••h2πrOSlr•hO'Or'2πr'rl2πr••hLOGO引入割圆术早在公元三世纪，我国数学家刘徽为推导圆的面积公式而发明了“倍边法割圆术”.他用加倍的方式不断增加圆内接正多边形的边数，使其面积与圆的面积之差更小，即所谓“割之弥细，所失弥小”.这样重复下去，就达到了“割之又割，以至于不可再割，则与圆合体而无所失矣”.这是世界上最早的“极限”思想.LOGO探究新知1.球的表面积设球的半径为R，它的表面积只与半径R有关，是以R为自变量的函数.事实上，如果球的半径为R，那么它的表面积是Or把一个半径为R的球的上半球横向切成n（无穷大）份，每份等高并且把每份看成一个类似圆柱，球的表面积为所有圆柱的侧面积之和.AOS球=4πR24倍大圆面积LOGO探究新知S球=4πR2把一个半径为R的球的上半球横向切成n(无穷大)份，每份等高并且把每份看成一个类似圆柱，其中半径等于底面圆半径，则从下到上第k个圆柱的侧面积为O'Ork••h•kh()2.kSkrh22()kRhrRkhn ,，2lim2[(1)(2)()]4.nSSSSnR球∴22222421()()2.RkSkRkhRnnn∴LOGO例题讲解例1如图，某种浮标由两个半球和一个圆柱黏合而成，半球的直径是0.3m，圆柱高0.6m．如果在浮标表面涂一层防水漆，每平方米需要0.5kg涂料，那么给1000个这样的浮标涂防水漆需要多少涂料？(π取3.14)解:一个浮标的表面积为2π×0.15×0.6+4π×0.152=0.8478(m2),所以给1000个这样的浮标涂防水漆约需涂料0.8478×0.5×1000=423.9(kg).LOGO类比利用圆周长求圆面积方法,我们可利用球的表面积求球的体积.如图,把球O的表面分成n个小网格,连接球心O和每个小网格的顶点,整个球体就被分割成n个“小锥体”.当n越大，每个小网格越小，每个“小椎体”的底面越平，“小椎体”就越接近似于棱锥，其高越近似于球的半径R.设O-ABCD是其中一个“小椎体”，那么它的体积就为探究新知OABCD2.球的体积问题1在小学,我们学习了圆的面积公式,你还记得是如何求得的吗?类比这种方法，你能由球的表面积公式推导出球的体积公式吗?πrr1.3OABCDABCDVSRLOGO探究新知OABCD1.3OABCDABCDVSR由于球的体积就是这n个“小椎体”的体积之和，而这n个“小椎体”的底面积这个...