8.3 简单几何体的表面积与体积(2个课时)（课件）-2022-2023学年高一数学同步精品课堂（人教A版2019必修第二册）.pptxVIP免费

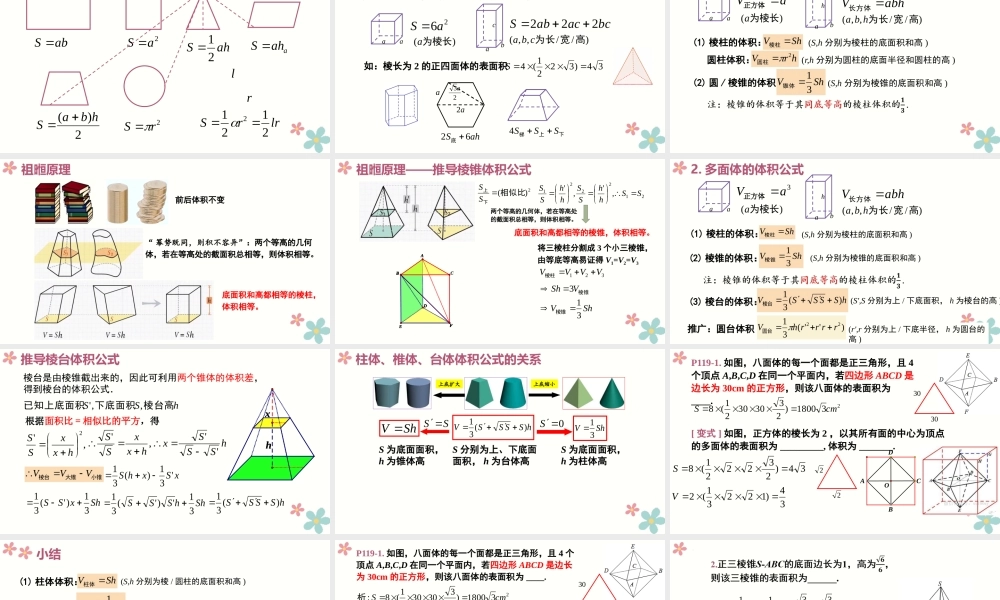
8.3简单几何体的表面积与体积预备知识——平面图形的面积abS2aSahS21aahS2)(hbaS2rSlrrS21212rl1.多面体的表面积公式26aSbcacabS222aac)(为棱长a)//,,(高宽为长cbaab多面体的表面积：围成它的各个面的面积之和。如：棱长为2的正四面体的表面积34)3221(4Sa223aa下上梯SSS4ahS62底2.多面体的体积公式3aV正方体abhV长方体aaabh)(为棱长a)//,,(高宽为长hbaShV棱柱(S,h分别为棱柱的底面积和高)(1)棱柱的体积：(2)圆/棱锥的体积：ShV31锥体(S,h分别为棱锥的底面积和高)圆柱体积：hrV2圆柱(r,h分别为圆柱的底面半径和圆柱的高)祖暅原理“幂势既同，则积不容异”：两个等高的几何体，若在等高处的截面积总相等，则体积相等。前后体积不变底面积和高都相等的棱柱，体积相等。DFBA祖暅原理——推导棱锥体积公式底面积和高都相等的棱锥，体积相等。两个等高的几何体，若在等高处的截面积总相等，则体积相等。DFABCEFBCAFDEB将三棱柱分割成3个小三棱锥，由等底等高易证得V1=V2=V3321VVVV棱柱棱锥VSh3ShV31棱锥2)(相似比下上SS212221,','SShhSShhSS2.多面体的体积公式3aV正方体abhV长方体aaabh)(为棱长a)//,,(高宽为长hbaShV棱柱(S,h分别为棱柱的底面积和高)(1)棱柱的体积：(2)棱锥的体积：ShV31棱锥(S,h分别为棱锥的底面积和高)(3)棱台的体积：hSSSSV)(31棱台(S',S分别为上/下底面积，h为棱台的高))''(3122rrrrhV圆台推广：圆台体积(r',r分别为上/下底半径，h为圆台的高)棱台是由棱锥截出来的，因此可利用两个锥体的体积差，得到棱台的体积公式．hhSS棱台高下底面积已知上底面积,,'hx,'2hxxSS,'hxxSShxhSSSx''推导棱台体积公式根据面积比=相似比的平方，得小锥大锥棱台VVVhSSSS)(31xSxhS'31)(31ShxSS31)'(31ShhSSS31')'(31S为底面面积，h为柱体高0SS分别为上、下底面面积，h为台体高SSS为底面面积，h为锥体高上底扩大上底缩小hSSSSV)(31ShVShV31柱体、椎体、台体体积公式的关系[变式]如图，正方体的棱长为2，以其所有面的中心为顶点的多面体的表面积为_________,体积为_______.2234)232221(8S34)12231(2VP119-1.如图，八面体的每一个面都是正三角形，且4个顶点A,B,C,D在同一个平面内，若四边形ABCD是边...