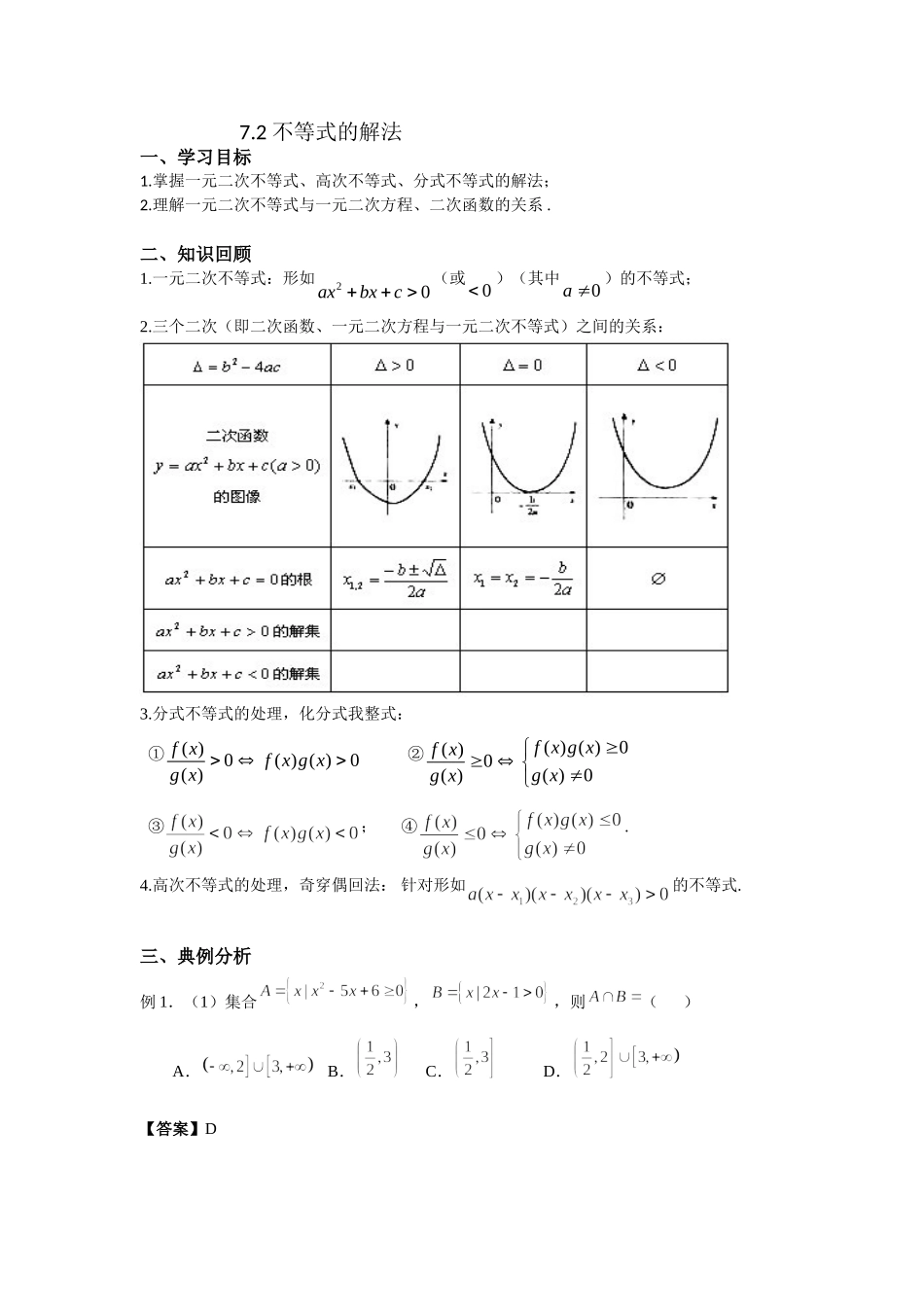
7.2不等式的解法一、学习目标1.掌握一元二次不等式、高次不等式、分式不等式的解法;2.理解一元二次不等式与一元二次方程、二次函数的关系.二、知识回顾1.一元二次不等式:形如20axbxc(或0)(其中0a)的不等式;2.三个二次(即二次函数、一元二次方程与一元二次不等式)之间的关系:3.分式不等式的处理,化分式我整式:①()0()()0()fxfxgxgx②()()0()0()0()fxgxfxgxgx③;④.4.高次不等式的处理,奇穿偶回法:针对形如的不等式.三、典例分析例1.(1)集合,,则()A.B.C.D.【答案】D(2)不等式(1)(2)(1)0xxx的解集为___________.【答案】(3)不等式的解集是________.【答案】(4)解不等式.【答案】不等式可化为,等价,于是.∴原不等式的解为或或.例2.(1)设一元二次不等式的解集为,则ab的值为()A.-6B.-5C.6D.5【答案】C(2)已知不等式20axbxc的解是2x或3x,求不等式20bxaxc的解。【答案】或.例3.(1)若不等式对任意实数均成立,则实数的取值范围是()A.B.C.D.【答案】C(2)若关于的不等式在区间上有解,则实数的取值范围为()A.B.C.(1,+∞)D.【答案】A【详解】因为,则不等式可化为:,设,由题意得只需,因为函数为区间上的减函数,所以.(3)若不等式对任意成立,则的取值范围为()A.B.C.D.【答案】A【详解】由题得不等式对任意成立,所以,即,解之得或.四、课外作业1.函数的定义域为()A.B.[1,3]C.D.[0,1]【答案】C2.不等式的解集为()A.B.C.D.【答案】C3.关于的不等式的解集()A.B.C.D.【答案】A4.已知不等式的解集为,则不等式的解集为()A.B.{或}C.D.或【答案】A5.关于x的不等式的解集为,且,则a=()A.B.C.D.【答案】A6.已知函数的值域为,若关于x的不等式的解集为,则实数c的值为__________.【答案】97.若函数的定义域为R,则实数的取值范围是________.【答案】8.若关于的不等式在区间[1,2]上有解,则的取值范围是________.【答案】9.已知函数,若对于任意的都有,则实数的取值范围为.【答案】10.若对于任意a[-1,1],函数f(x)=x+(a-4)x+4-2a的值恒大于零,则x的取值范围是.【答案】(-∞‚1)(3,+∞)∪11.已知关于的不等式的解集为.(1)当时,求集合;(2)当且时,求实数的取值范围.【答案】(1)或;(2)【详解】(1)当时,,所以或;(2)因为,所以,得或,又因为,所以不成立,即,解得,综上...