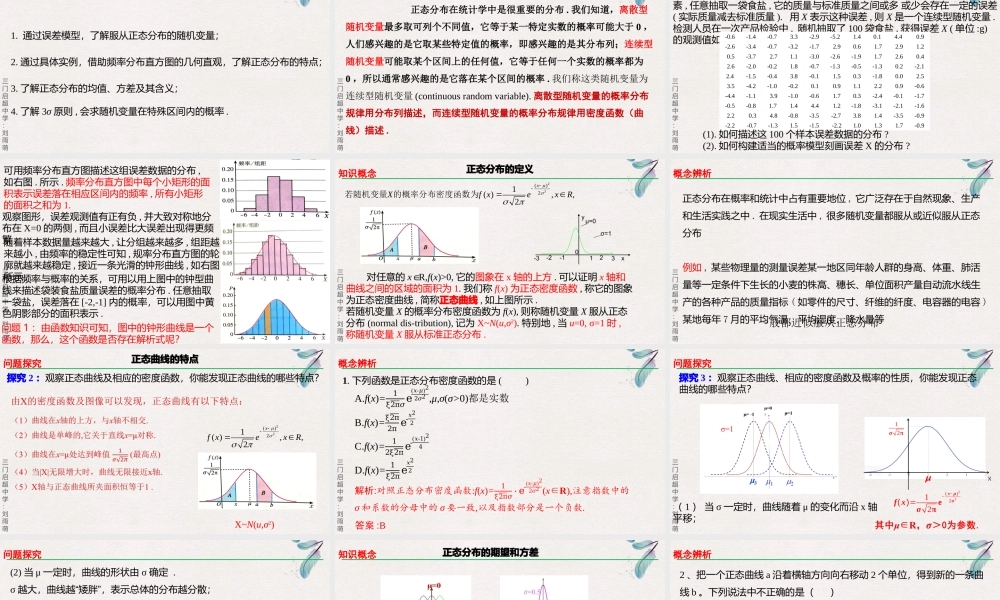
第七章随机变量及其分布7.5正态分布高斯是一个伟大的数学家,一生中的重要贡献不胜枚举.德国的10马克纸币上印有高斯的头像和正态分布的曲线,这就传达了一个信息:在高斯的科学贡献中,对人类文明影响最大的是正态分布.三门启超中学:刘雨萌学习目标1.通过误差模型,了解服从正态分布的随机变量;2.通过具体实例,借助频率分布直方图的几何直观,了解正态分布的特点;3.了解正态分布的均值、方差及其含义;4.了解3σ原则,会求随机变量在特殊区间内的概率.三门启超中学:刘雨萌问题导学正态分布在统计学中是很重要的分布.我们知道,离散型随机变量最多取可列个不同值,它等于某一特定实数的概率可能大于0,人们感兴趣的是它取某些特定值的概率,即感兴趣的是其分布列;连续型随机变量可能取某个区间上的任何值,它等于任何一个实数的概率都为0,所以通常感兴趣的是它落在某个区间的概率.我们称这类随机变量为连续型随机变量(continuousrandomvariable).离散型随机变量的概率分布规律用分布列描述,而连续型随机变量的概率分布规律用密度函数(曲线)描述.三门启超中学:刘雨萌问题探究探究1:自动流水线包装的食盐,每袋标准质量为400g.由于各种不可控的因素,任意抽取一袋食盐,它的质量与标准质量之间或多或少会存在一定的误差(实际质量减去标准质量).用X表示这种误差,则X是一个连续型随机变量.检测人员在一次产品检验中,随机抽取了100袋食盐,获得误差X(单位:g)的观测值如下:-0.6-1.4-0.73.3-2.9-5.21.40.14.40.9-2.6-3.4-0.7-3.2-1.72.90.61.72.91.20.5-3.72.71.1-3.0-2.6-1.91.72.60.42.6-2.0-0.21.8-0.7-1.3-0.5-1.30.2-2.12.4-1.5-0.43.8-0.11.50.3-1.80.02.53.5-4.2-1.0-0.20.10.91.12.20.9-0.6-4.4-1.13.9-1.0-0.61.70.3-2.4-0.1-1.7-0.5-0.81.71.44.41.2-1.8-3.1-2.1-1.62.20.34.8-0.8-3.5-2.73.81.4-3.5-0.9-2.2-0.7-1.31.5-1.5-2.21.01.31.7-0.9(1).如何描述这100个样本误差数据的分布?(2).如何构建适当的概率模型刻画误差X的分布?三门启超中学:刘雨萌可用频率分布直方图描述这组误差数据的分布,如右图.所示.频率分布直方图中每个小矩形的面积表示误差落在相应区间内的频率,所有小矩形的面积之和为1.观察图形,误差观测值有正有负,并大致对称地分布在X=0的两侧,而且小误差比大误差出现得更频繁.随着样本数据量越来越大,让分组越来越多,组距越来越小,由频率的稳定性可知,规率分布直方图的轮廓就越来越稳定,接近一条光滑的钟形曲线,如右图所...