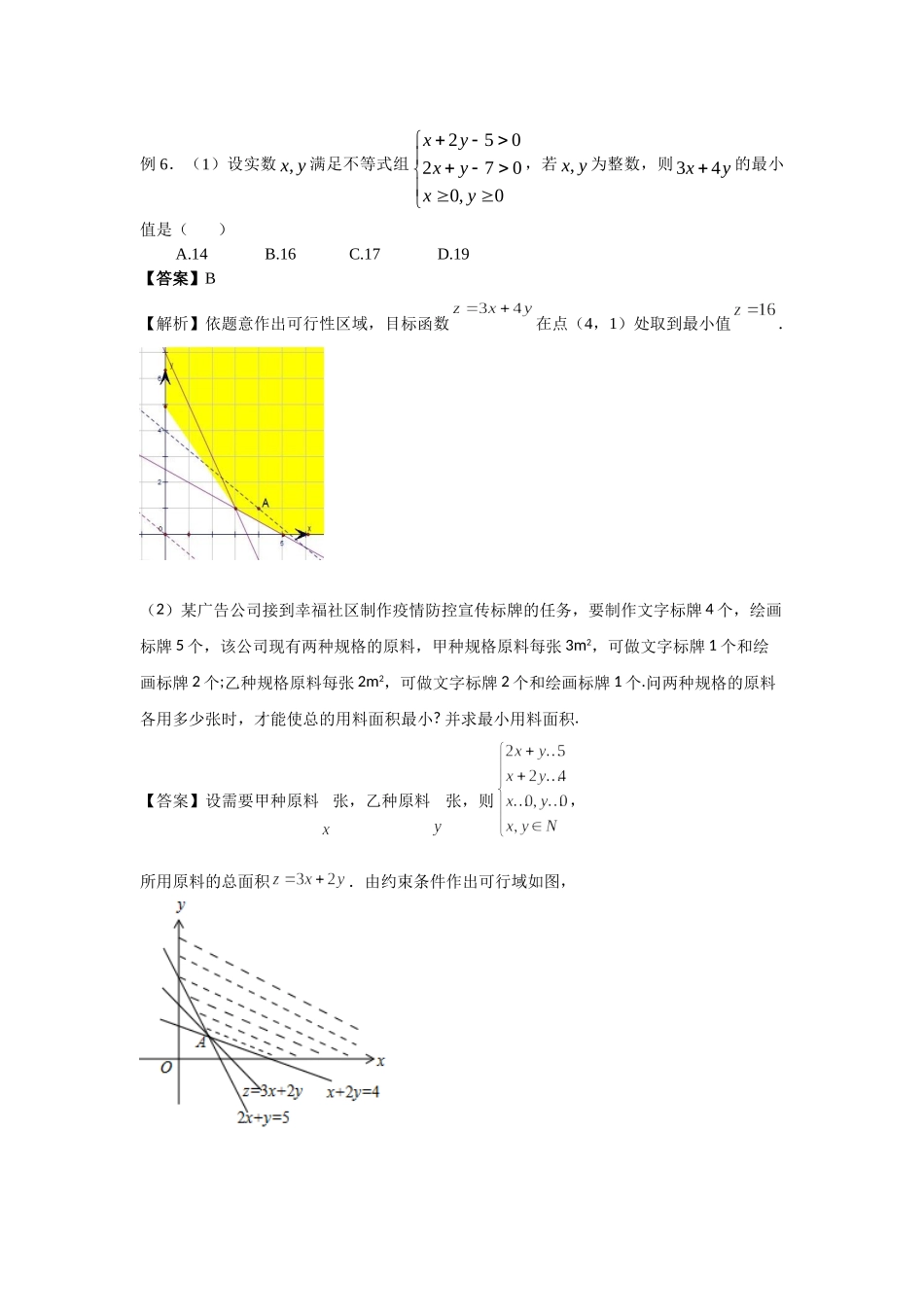
7.3二元一次不等式(组)及简单的线性规划问题一、学习目标1.理解二元一次不等式(组)与平面区域的关系;2.掌握简单的线性规划问题;3.了解常见的非线性目标函数的几何含义.二、知识回顾1.二元一次不等式表示直线某一侧的平面区域;2.线性规划的有关概率:名称含义约束条件由变量,组成的不等式(组)线性约束条件由变量,组成的二元一次不等式(组)目标函数由变量,组成的二元函数线性目标函数目标函数形如可行解满足约束条件的解可行域所有可行解的集合最优解使得目标函数取到最值的可行解线性规划问题在线性约束条件下求线性目标函数的最值问题3.利用线性规划求目标函数最值的步骤①画出约束条件对应的可行域;②将目标函数视为动直线,并将其平移经过可行域,找到最优解对应的点;③将最优解代入目标函数,求出最大值或最小值.常见的目标函数有:()ⅰ截距型:形如z=ax+by;()ⅱ距离型:形如z=;()ⅲ斜率型:形如z=.三、典例分析例1.(1)在平面直角坐标系中,不等式组所表示的平面区域的面积是______;(2)若不等式组表示的平面区域是一个三角形,则a的取值范围是________.【答案】(1)4;(2)(0,1][∪,+∞).例2.(1)若实数x,y满足约束条件,则z=x+2y的取值范围是()A.(-∞,4]B.[4,+∞)C.[5,+∞)D.(-∞,+∞)(2)若实数x,y满足约束条件,则的最小值是()A.B.C.D.【答案】(1)B;(2)B.例3.(1)若实数,xy满足不等式组33023010xyxyxmy,且xy的最大值为9,则实数m____.(2)设zkxy,其中实数,xy满足20240240xyxyxy,若z的最大值为12,则实数k____.【答案】(1);(2)2.例4.(1)已知x,y满足则的取值范围为__________.(2)已知实数x,y满足则x2+(y+1)2的最小值为_______.【答案】(1);(2).例5.(1)若0,0ab,且当001xyxy时,恒有1axby,则以,ab为坐标的点(,)Pab所形成的平面区域的面积是______.若实数,xy满足240101xyxyx,14axy恒成立,则实数a的取值范围是_______.【答案】(1)1;(2).例6.(1)设实数,xy满足不等式组2502700,0xyxyxy,若,xy为整数,则34xy的最小值是()A.14B.16C.17D.19【答案】B【解析】依题意作出可行性区域,目标函数在点(4,1)处取到最小值.(2)某广告公司接到幸福社区制作疫情防控宣传标牌的任...