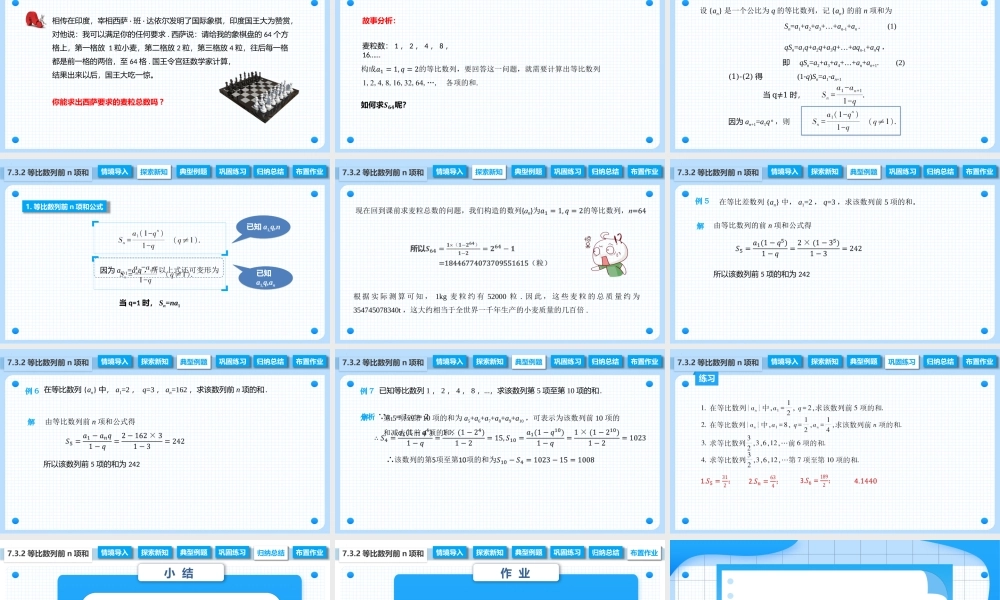
7.3.2等比数列的前n项和公式中职数学拓展模块一下册探索新知典型例题巩固练习归纳总结布置作业情境导入情境导入相传在印度,宰相西萨·班·达依尔发明了国际象棋,印度国王大为赞赏,对他说:我可以满足你的任何要求.西萨说:请给我的象棋盘的64个方格上,第一格放1粒小麦,第二格放2粒,第三格放4粒,往后每一格都是前一格的两倍,至64格.国王令宫廷数学家计算,结果出来以后,国王大吃一惊。7.3.2等比数列前n项和你能求出西萨要求的麦粒总数吗?情境导入典型例题巩固练习归纳总结布置作业情境导入探索新知7.3.2等比数列前n项和故事分析:麦粒数:1,2,4,8,16……情境导入典型例题巩固练习归纳总结布置作业情境导入探索新知7.3.2等比数列前n项和设{an}是一个公比为q的等比数列,记{an}的前n项和为qSn=a1q+a2q+a3q+…+aqn-1+anq,即qSn=a2+a3+a4+…+an+an+1.(2)(1)-(2)得(1-q)Sn=a1-an+1Sn=a1+a2+a3+…+an-1+an.(1)当q≠1时,因为an+1=a1qn,则情境导入典型例题巩固练习归纳总结布置作业情境导入探索新知7.3.2等比数列前n项和1.等比数列前n项和公式因为an+1=anq,所以上式还可变形为已知a1,q,n已知a1,q,an当q=1时,Sn=na1情境导入典型例题巩固练习归纳总结布置作业情境导入探索新知7.3.2等比数列前n项和根据实际测算可知,1kg麦粒约有52000粒.因此,这些麦粒的总质量约为354745078340t,这大约相当于全世界一千年生产的小麦质量的几百倍.情境导入典型例题情境导入探索新知巩固练习归纳总结布置作业例57.3.2等比数列前n项和在等比差数列{an}中,a1=2,q=3,求该数列前5项的和.解由等比数列的前n项和公式得所以该数列前5项的和为242情境导入典型例题情境导入探索新知巩固练习归纳总结布置作业例67.3.2等比数列前n项和在等比数列{an}中,a1=2,q=3,an=162,求该数列前n项的和.解由等比数列前n项和公式得所以该数列前5项的和为242情境导入典型例题情境导入探索新知巩固练习归纳总结布置作业例77.3.2等比数列前n项和已知等比数列1,2,4,8…,,求该数列第5项至第10项的和.分析第5项至第10项的和为a5+a6+a7+a8+a9+a10,可表示为该数列前10项的和减去其前4项的和.解情境导入巩固练习情境导入探索新知典型例题归纳总结布置作业练习7.3.2等比数列前n项和情境导入归纳总结情境导入探索新知典型例题巩固练习布置作业小结7.3.2等比数列前n项和情境导入布置作业情境导入探索新知典型例题巩固练习归纳总结作业7.3.2等比数列前n项和1.书面作业:完成教材第72页习题7.3;2.查漏补缺:根据个人情况对课堂学习复习与回顾;3.拓展作业:阅读教材扩展延伸内容.本节课堂结束.教师:姜老师