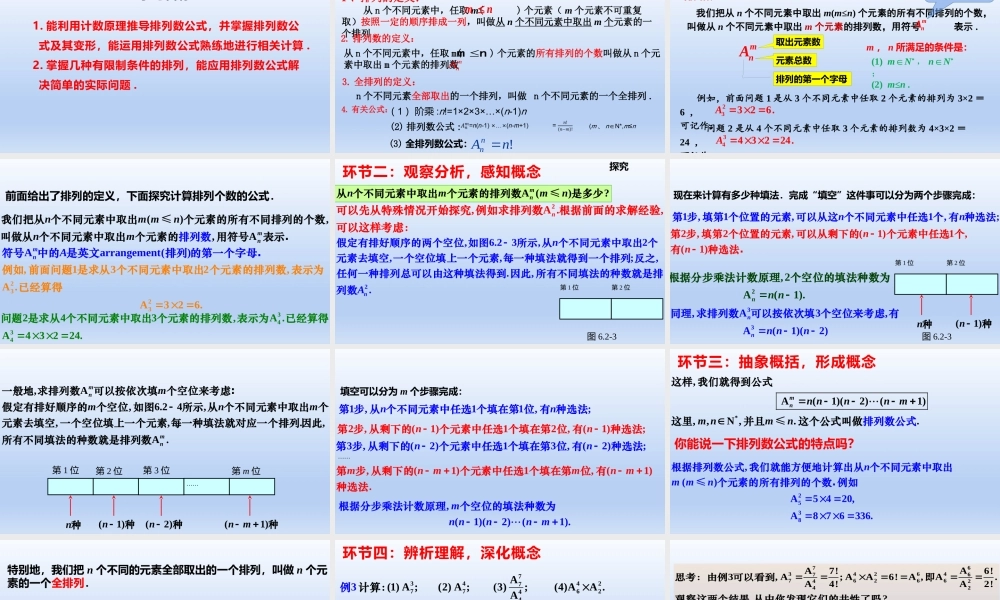
人教A版2019选择性必修第三册1.能利用计数原理推导排列数公式,并掌握排列数公式及其变形,能运用排列数公式熟练地进行相关计算.2.掌握几种有限制条件的排列,能应用排列数公式解决简单的实际问题.学习目标从n个不同元素中,任取m()个元素(m个元素不可重复取)按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.nm1、排列的定义:2.排列数的定义:从n个不同元素中,任取m()个元素的所有排列的个数叫做从n个元素中取出m个元素的排列数nmmnA3.全排列的定义:n个不同元素全部取出的一个排列,叫做n个不同元素的一个全排列.4.有关公式:(3)全排列数公式:!nAnn(2)排列数公式:(1)阶乘:n!=1×2×3×…×(n-1)n(m、nN*,∈m≤n环节一:创设情境,引入课题前面给出了排列的定义,下面探究计算排列个数的公式.排列数:我们把从n个不同元素中取出m(m≤n)个元素的所有不同排列的个数,叫做从n个不同元素中取出m个元素的排列数,用符号表示.mnA排列的第一个字母元素总数取出元素数m,n所满足的条件是:(1)m∈N*,n∈N*;(2)m≤n.mnA例如,前面问题1是从3个不同元素中任取2个元素的排列为3×2=6,可记作:23326.A问题2是从4个不同元素中任取3个元素的排列数为4×3×2=24,可记作3443224.A符号中的A是英文arrangement(排列)的第一个字母mnA前面给出了排列的定义,下面探究计算排列个数的公式.()A,,mnmmnmnn我们把从个不同元素中取出个元素的所有不同排列的个数排列叫做从个不同元素中取出个元素的用符号数表示.≤Aarrangement()mnA符号中的是英文排列的第一个字母.2323,132,A.A326.例如前面问题是求从个不同元素中取出个元素的排列数表示为已经算得3434243,A.A43224.问题是求从个不同元素中取出个元素的排列数表示为已经算得探究A()?mnmnmn从个不同元素中取出个元素的排列数是多少≤第1位第2位图6.2-32,A.,n可以先从特殊情况开始探究例如求排列数根据前面的求解经验可以这样考虑:2,6.23,2,,;,.,.nnA假定有排好顺序的两个空位如图所示从个不同元素中取出个元素去填空一个空位填上一个元素每一种填法就得到一个排列反之任何一种排列总可以由这种填法得到因此所有不同填法的种数就是排列数环节二:观察分析,感知概念第1位第2位n种(1)n种图6.2-3现在来计算有多少种填法.完成“填空”这件事可以分为两个步骤完成:1,1,1,;nn第步填第个位置的元素可以从这个不同元素中任选个有种选法2,2,(1)1,(1)nn...