6.2.1直线的的倾斜角与斜率（PPT）-【中职专用】高一数学同步精品课堂（高教版2021·基础模块下）.pptxVIP免费

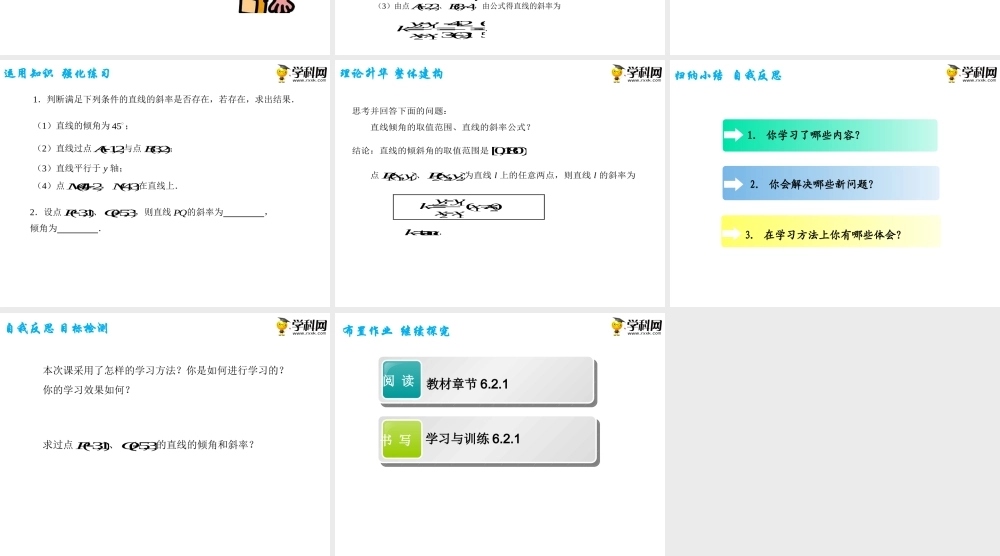
6.2.1直线的的倾斜角与斜率第六章直线与圆的方程创设情景兴趣导入问题问题123lll、、如图所示，直线虽然都经过点P，但是它们对x轴的倾斜程度是不同的．为了确定直线对x轴的倾斜程度，我们引入直线的倾斜角的概念．动脑思考探索新知为了确定直线对x轴的倾斜程度，我们引入直线的倾斜角的概念．当直线l与x轴相交时，直线l向上的方向与x轴正方向所成的最小正角α，称为直线l的倾斜角，若直线l平行于x轴，规定倾斜角为零，这样，对任意的直线，均有0≤180．OABPxyPABOxy如何根据直线上的任意两个点的坐标来确定倾角的大小．111222(,)(,)PxyPxy、设为直线l上的任意两点，可以得到12xx，2121tanyyxx90当时，9012xxtan时，，的值不存在，此时直线l与x轴垂直.当动脑思考探索新知动脑思考探索新知90l倾角的正切值叫做直线的斜率，用小写字母k表示，即tank．111222(,)(,)PxyPxy、设点为直线l上的任意两点，则直线l的斜率为211221()yykxxxx12PP、当的纵坐标相同时，斜率是否存在？倾斜角是多少？巩固知识典型例题例1根据下面各直线满足的条件，分别求出直线的斜率：（1）直线与x轴平行；（2）直线倾斜角为4；（2）直线过点(2,2)A与点(3,4)B．解（1）因为直线与x轴平行，倾斜角0，所以直线的斜率为tan00k（2）由于倾斜角4，故直线的斜率为tantan14k．（3）由点(2,2)A、(3,4)B，由公式得直线的斜率为21214263(2)5yykxx．巩固知识典型例题例2已知直线的斜率为-1，求直线的倾斜角。解因为直线的斜率tan=-1k，且0，所以直线的倾斜角3=4.运用知识强化练习1．判断满足下列条件的直线的斜率是否存在，若存在，求出结果．（1）直线的倾角为45；（2）直线过点(1,2)A与点(3,2)B；（3）直线平行于y轴；（4）点(4,2)M，(4,3)N在直线上．2．设点(3,1)P、(5,3)Q，则直线PQ的斜率为，倾角为．思考并回答下面的问题：直线倾角的取值范围、直线的斜率公式？结论：直线的倾斜角的取值范围是[0,180)点111(,)Pxy、222(,)Pxy为直线l上的任意两点，则直线l的斜率为211221()yykxxxx．tank．理论升华整体建构3.在学习方法上你有哪些体会？2.你会解决哪些新问题？1.你学习了哪些内容？归纳小结自我反思本次课采用了怎样的学习方法？你是如何进行学习的？你的学习效果如何？求过点(3,1)P、(5,3)Q的直线的倾角和斜率？自我反思目标检测布置作业继续探究阅读教材章节6.2.1书写学习与训练6.2.1