6.2.4 向量的数量积(2个课时)（课件）-2022-2023学年高一数学同步精品课堂（人教A版2019必修第二册）.pptxVIP免费

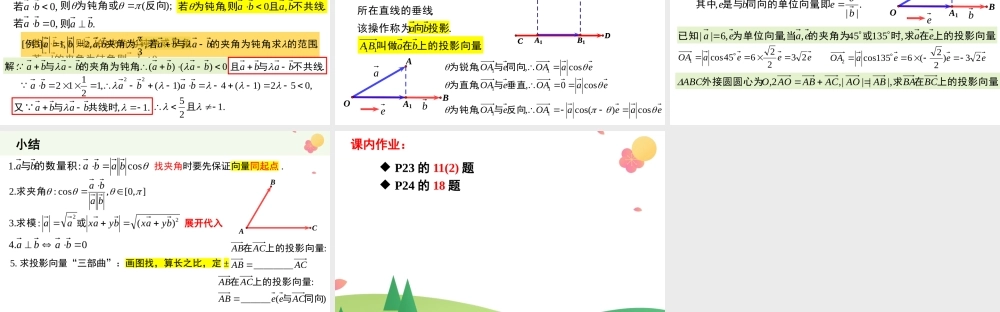
必修2《第六章平面向量及其应用》6.2.4向量的数量积如图所示，一个力F作用于一个物体，使该物体发生了位移s，力F与位移s的夹角是θ，如何计算这个力所做的功？θFs新知引入：cosFsWcossFW)(的夹角与为sF向量的数量积的物理背景cosbaba新知1：向量的数量积(或内积)运算cos:bababa的数量积与非零向量,:的夹角与为①注baAOBbOBaOA则作,,].,0[找两向量夹角时要先保证向量同起点.OABab]1,1[cosbaba同向②ba,:0反向ba,:ba:20ba),(为非零向量bababababa③向量的数量积是实数；“·”不可省略.cosθ=1cosθ=-1.00,0,,:babababa或或则若对于任意向量注baba,,记作的夹角新知1：向量的数量积(或内积)运算cos:bababa的数量积与非零向量)0,(cos:bababa⑤求夹角2sin,tan,sin,cos可求由2:aa⑥求模20cos:aaaaa原理OABaba0:④规定是一实数ba00:a区分是一个向量a02aaa记作22aa2)(babababa222判断正误：向量数量积的理解.,0baba则①若.00,0bababa或或则若.,bacbca则②若.,,0的夹角为钝角则③若baba.0,,baba则的夹角为钝角④若cos||||cos||||cbca钝角或平角.,22baba则⑤若但方向可能不同,ba).()(cbacba⑥不一定共线但ca,;)(共线的向量表示与ccba;)(共线的向量表示与acba巩固：向量的数量积运算.,8,5,60,]1[CABCbaCABC求中已知例.22912254||||cos:baba解.65],,0[.20)21(85120cos:CABCCABC解.,32,4,5]9[bababa求的夹角与已知例.,254,9,12]10[的夹角与求设例bababa5ABC510)21(45cos:baba解P17P18新知2：向量数量积的运算律abba:①交换律)()()(:bababa②结合律cbcacba)(:③分配律222)(bbaaba④22)()(bababa).2()3(,60,2,3]12[babababa求夹角为与若例P20P21,3212360cos:baba由题意得解babababa226)2()3(32632212新知2：向量数量积的运算律.,___,,,4,3]13[垂直与时则不共线且已知例bkabkakbaba.||,72)3()2(,4||60,]2[abababba求且夹角为若例726:22bbaa思路729622...