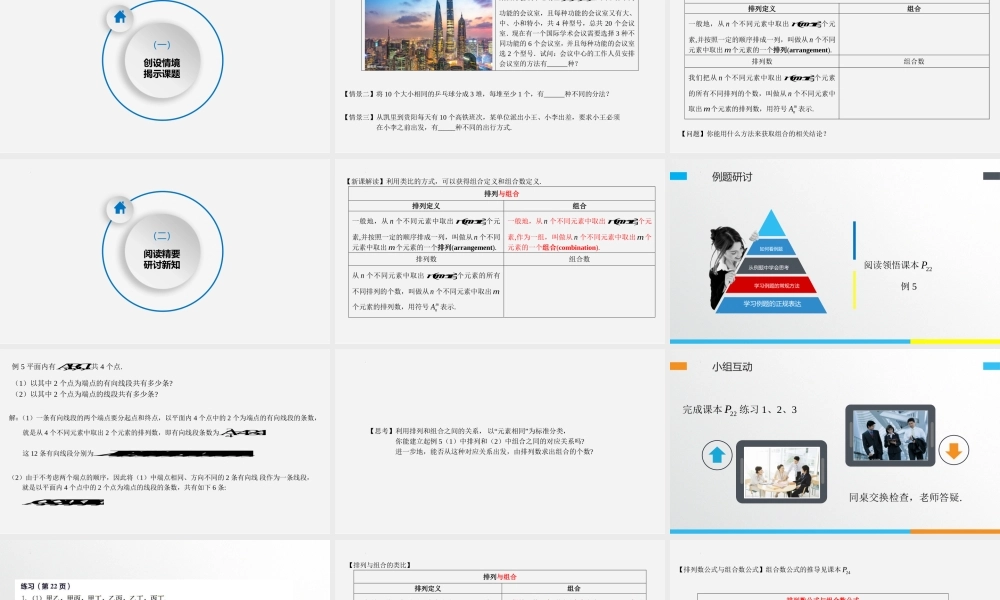
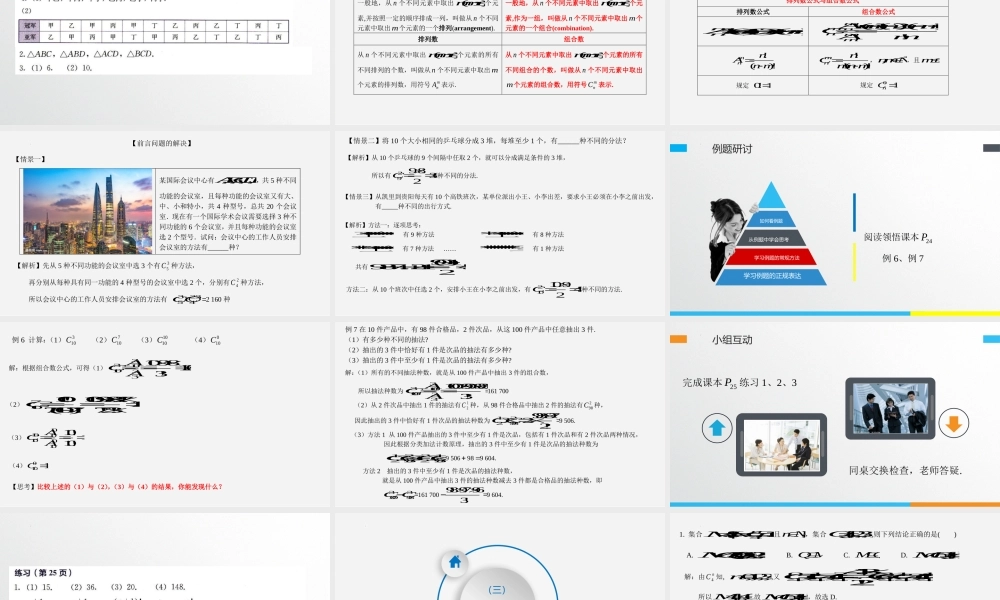
6.2.3组合6.2.4组合数公式第六章计数原理凯里一中尹洪January26,2025(一)创设情境揭示课题【情景一】某国际会议中心有,,,,ABCDE,共5种不同功能的会议室,且每种功能的会议室又有大、中、小和特小,共4种型号,总共20个会议室.现在有一个国际学术会议需要选择3种不同功能的6个会议室,并且每种功能的会议室选2个型号.试问:会议中心的工作人员安排会议室的方法有______种?【情景二】将10个大小相同的乒乓球分成3堆,每堆至少1个,有______种不同的分法?【情景三】从凯里到贵阳每天有10个高铁班次,某单位派出小王、小李出差,要求小王必须在小李之前出发,有_____种不同的出行方式.【回顾】排列与组合排列定义组合一般地,从n个不同元素中取出()mmn个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列(arrangement).排列数组合数我们把从n个不同元素中取出()mmn个元素的所有不同排列的个数,叫做从n个不同元素中取出m个元素的排列数,用符号mnA表示.【问题】你能用什么方法来获取组合的相关结论?(二)阅读精要研讨新知【新课解读】利用类比的方式,可以获得组合定义和组合数定义.排列与组合排列定义组合一般地,从n个不同元素中取出()mmn个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列(arrangement).一般地,从n个不同元素中取出()mmn个元素,作为一组,叫做从n个不同元素中取出m个元素的一个组合(combination).排列数组合数从n个不同元素中取出()mmn个元素的所有不同排列的个数,叫做从n个不同元素中取出m个元素的排列数,用符号mnA表示.例题研讨学习例题的正规表达学习例题的常规方法从例题中学会思考如何看例题阅读领悟课本22P例5例5平面内有,,,ABCD共4个点.(1)以其中2个点为端点的有向线段共有多少条?(2)以其中2个点为端点的线段共有多少条?解:(1)一条有向线段的两个端点要分起点和终点,以平面内4个点中的2个为端点的有向线段的条数,就是从4个不同元素中取出2个元素的排列数,即有向线段条数为244312A这12条有向线段分别为,,,,,,,,,,,ABBAACCAADDABCCBBDDBCDDC��.(2)由于不考虑两个端点的顺序,因此将(1)中端点相同、方向不同的2条有向线段作为一条线段,就是以平面内4个点中的2个点为端点的线段的条数,共有如下6条:,,,,,ACACADBCBDCD【思考】利用排列和组合之间的关系,以“元素相同”为标准分类,你能建立起例5(1)中排列和(2)中组合之同的...