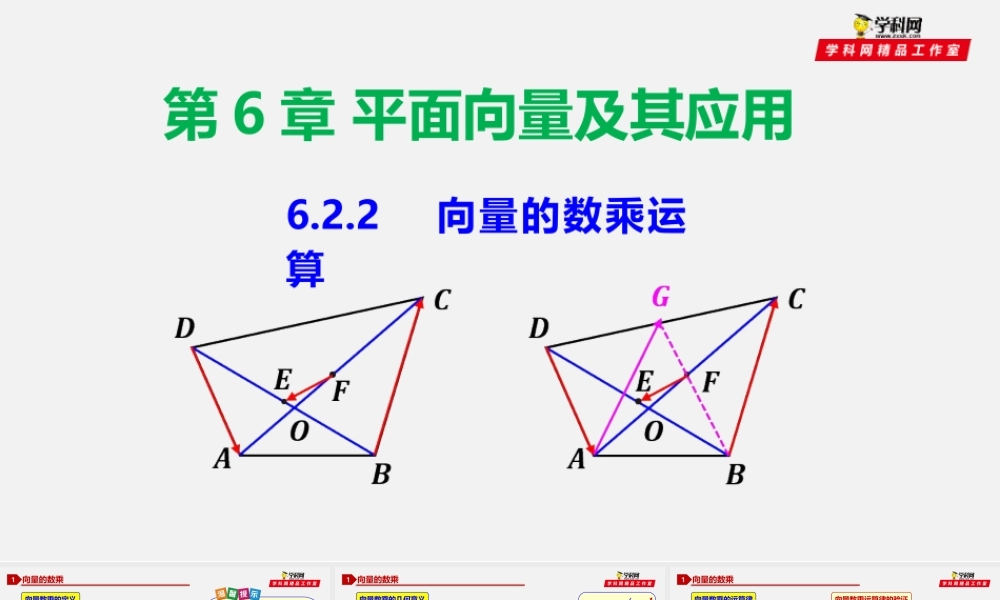
第6章平面向量及其应用6.2.2向量的数乘运算☆当时,的方向和的方向相同;当时,的方向和的方向相反;当时向量的数乘1向量数乘的定义★一般地,我们规定实数和向量的积是一个向量,这种运算叫做向量的数乘,记作,它的长度和方向规定如下:☆①向量数乘的结果仍然是向量,这个向量的长度、方向都和以及有关;②实数和向量可以相乘,但不能相加减,,无意义;③表示和向量方向相同的单位向量④根据向量的数乘运算,向量与的方向相同或相反.向量的数乘1向量数乘的几何意义如图,在向量数乘中,可视为将向量的长度伸长或缩短的倍数.的符号表示是够改变向量的方向,当时,向量的方向和相同;当时,向量的方向和向量相反;当时,向量理解意义常见的误区当或时,均有,反之亦成立,即容易出错的是当或的时候,误将当成实数0向量的数乘1向量数乘的运算律设,为向量,,为实数,则:(1)(2)(3)特别地,有向量数乘运算律的验证以(1)为例验证:若或或,显然成立;若且且,则根据向量数乘的定义有,以及①②③即与的模长相等.综上,注意,,这些特殊情况及,同号、异号的情况.★第二分配率的几何意义:将表示向量,的有向线段先相加,再伸长或缩短倍,与将表示向量,的有向线段先伸长或缩短至原来的倍后再相加,所得的结果相同.★结合率的几何意义:将表示向量的有向线段先伸长或缩短至原来的倍,再伸长或缩短倍,与将表示向量的有向线段伸长或缩短至原来的倍所得的结果相同.向量的数乘1运算律的几何意义以为例,解释如下:★第一分配率的几何意义:将表示向量的有向线段伸长或缩短至原来的倍,与将表示向量的有向线段先伸长或缩短至原来的倍后,在与表示向量的有向线段伸长或缩短至原来的倍后相加所得的结果相同.化简下列各式:【解】(1)原式=(2)原式=向量的线性运算2向量的加法、减法、数乘运算统称为向量的线性运算,线性运算的结果还是向量.对于任意向量,,以及任意实数,,,恒有以下等式成立:线性运算难点点拨【1】向量的线性运算类似于代数多项式的运算,主要是“合并同类项”“提取公因式”,只不过这里的“同类项”“公因式”都是向量,实数可以看做是向量的系数.【2】对于向量的线性运算,关键是把握运算顺序,即先根据运算律去括号,再进行数乘运算,最后进行向量的加减,即“先乘除,后加减”.向量共线定理3向量与共线的充要条件是:存在唯一一个实数,使向量共线定理理解点拨★向量共线定理中规定的原因:①若将去掉,则当时,显然和共线;...