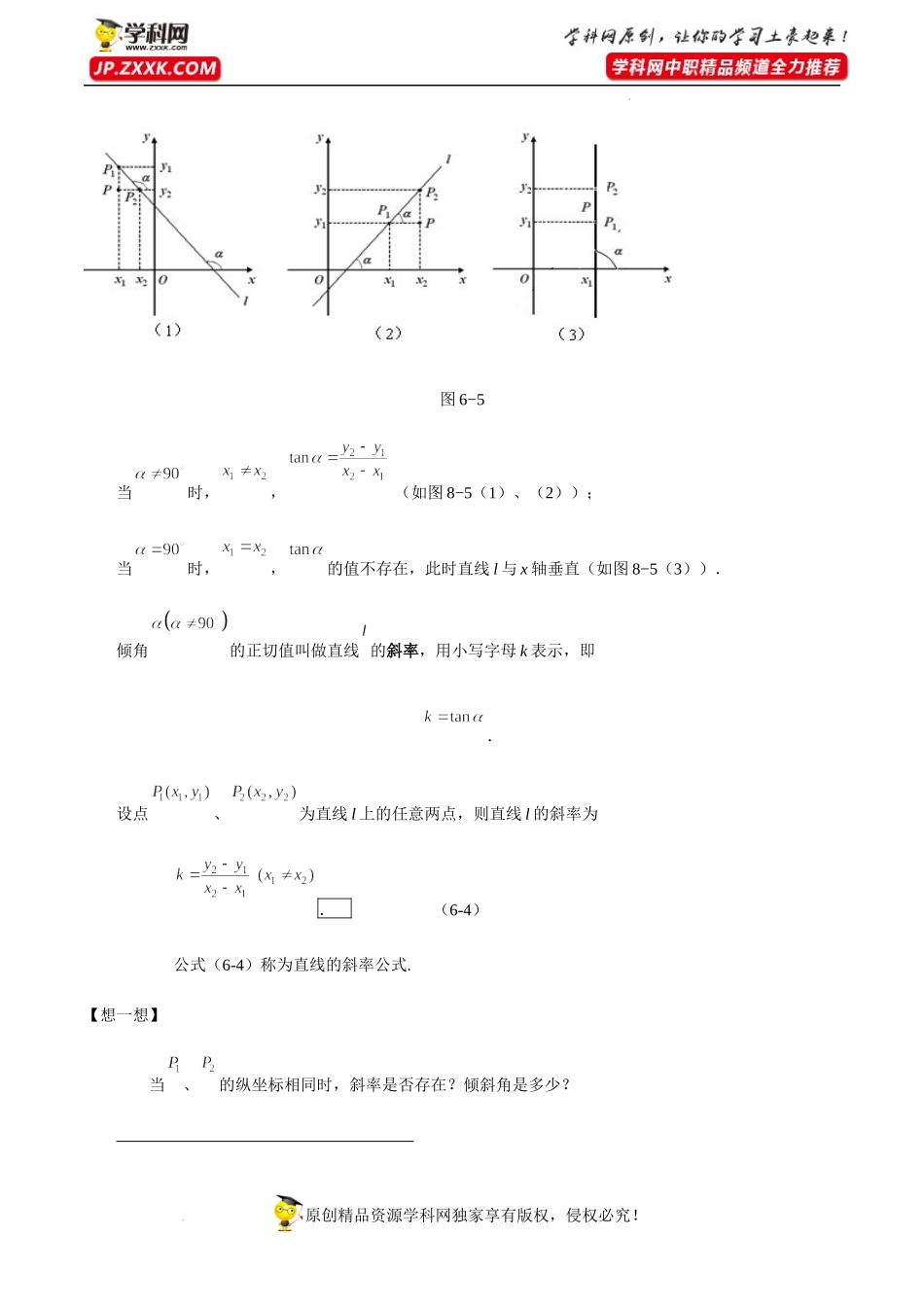
原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司6.2.1直线的的倾斜角与斜率【教学目标】知识目标:(1)理解直线的倾角、斜率的概念;(2)掌握直线的倾角、斜率的计算方法.能力目标:会应用斜率公式求直线的斜率及倾斜角,从而培养学生的数学思维能力和计算技能.情感目标:经历斜率公式的分析讨论过程,培养学生的有序思维的良好习惯.【教学重点】直线的斜率公式的应用.【教学难点】直线的斜率概念和公式的理解.【教学备品】教学课件.【课时安排】2课时.(90分钟)【教学过程】创设情境兴趣导入原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司【问题】如图所示,直线、、虽然都经过点P,但是它们相对于x轴的倾斜程度是不同的.教学意图:从实例出发使学生自然的走向知识点动脑思考探索新知【新知识】为了确定直线对x轴的倾斜程度,我们引入直线的倾斜角的概念.当直线l与x轴相交时,直线l向上的方向与x轴正方向所成的最小正角α,称为直线l的倾斜角,若直线l平行于x轴,规定倾斜角为零,这样,对任意的直线,均有≤.教学意图:带领学生分析下面研究如何根据直线上的任意两个点的坐标来确定倾角的大小.设、为直线l上的任意两点,可以得到yxOBAPyxPBAO原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司图6−5当时,,(如图8−5(1)、(2));当时,,的值不存在,此时直线l与x轴垂直(如图8−5(3)).倾角的正切值叫做直线的斜率,用小写字母k表示,即.设点、为直线l上的任意两点,则直线l的斜率为.(6-4)公式(6-4)称为直线的斜率公式.【想一想】当、的纵坐标相同时,斜率是否存在?倾斜角是多少?原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司教学意图:引导式启发学生得出结果巩固知识典型例题例1根据下面各直线满足的条件,分别求出直线的斜率:(1)直线与x轴平行;(2)直线倾斜角为;(2)直线过点与点.解(1)因为直线与x轴平行,倾斜角,所以直线的斜率为(2)由于倾斜角,故直线的斜率为.(3)由点、,由公式得直线的斜率为.说明利用公式6-4计算直线的斜率时,将哪个点看作为,哪个点看作为并不影响计算结果.【想一想】你能求出例1(2)中直线的倾斜角吗?原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司例2已知直线的斜率为-1,求直线的倾斜角。解因为直线的斜率,且,所以直线的倾斜角.教学意图...