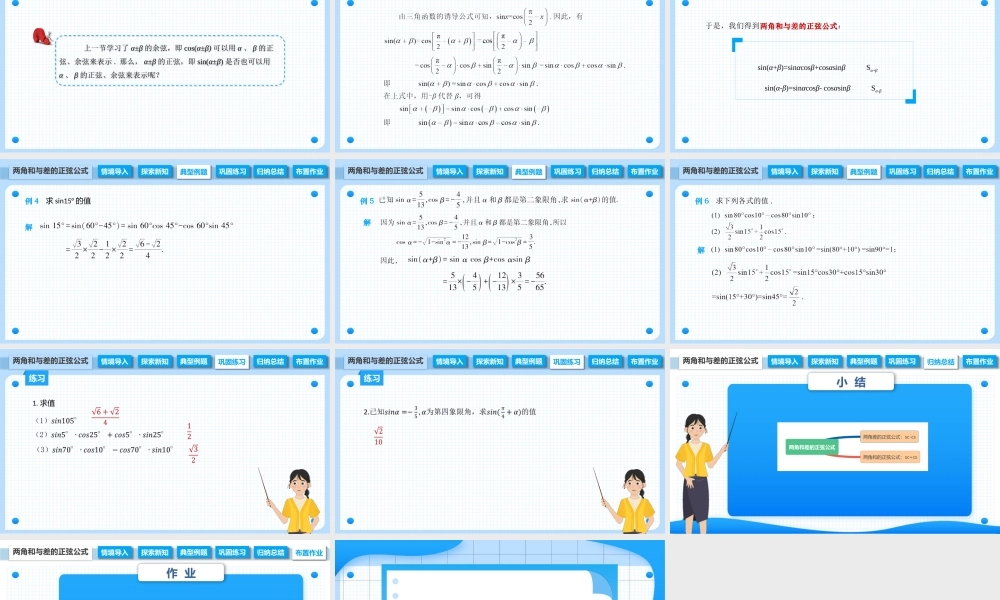
6.1.2两角和与差的正弦公式中职数学拓展模块一上册探索新知典型例题巩固练习归纳总结布置作业两角和与差的正弦公式情境导入情境导入上一节学习了α±β的余弦,即cos(α±β)可以用α、β的正弦、余弦来表示.那么,α±β的正弦,即sin(α±β)是否也可以用α、β的正弦、余弦来表示呢?情境导入典型例题巩固练习归纳总结布置作业两角和与差的正弦公式情境导入探索新知情境导入典型例题巩固练习归纳总结布置作业两角和与差的正弦公式情境导入探索新知于是,我们得到两角和与差的正弦公式:sin(α+β)=sinαcosβ+cosαsinβSα+βsin(α-β)=sinαcosβ-cosαsinβSα-β情境导入典型例题情境导入探索新知巩固练习归纳总结布置作业两角和与差的正弦公式例4求sin15°的值解情境导入典型例题情境导入探索新知巩固练习归纳总结布置作业两角和与差的正弦公式例5解情境导入典型例题情境导入探索新知巩固练习归纳总结布置作业两角和与差的正弦公式例6求下列各式的值.解情境导入巩固练习情境导入探索新知典型例题归纳总结布置作业练习两角和与差的正弦公式1.求值情境导入巩固练习情境导入探索新知典型例题归纳总结布置作业练习两角和与差的正弦公式情境导入归纳总结情境导入探索新知典型例题巩固练习布置作业两角和与差的正弦公式小结情境导入布置作业情境导入探索新知典型例题巩固练习归纳总结两角和与差的正弦公式作业1.书面作业:完成教材第7页练习6.1.2;2.查漏补缺:根据个人情况对课堂学习复习与回顾;3.拓展作业:阅读教材扩展延伸内容.本节课堂结束.教师:姜老师