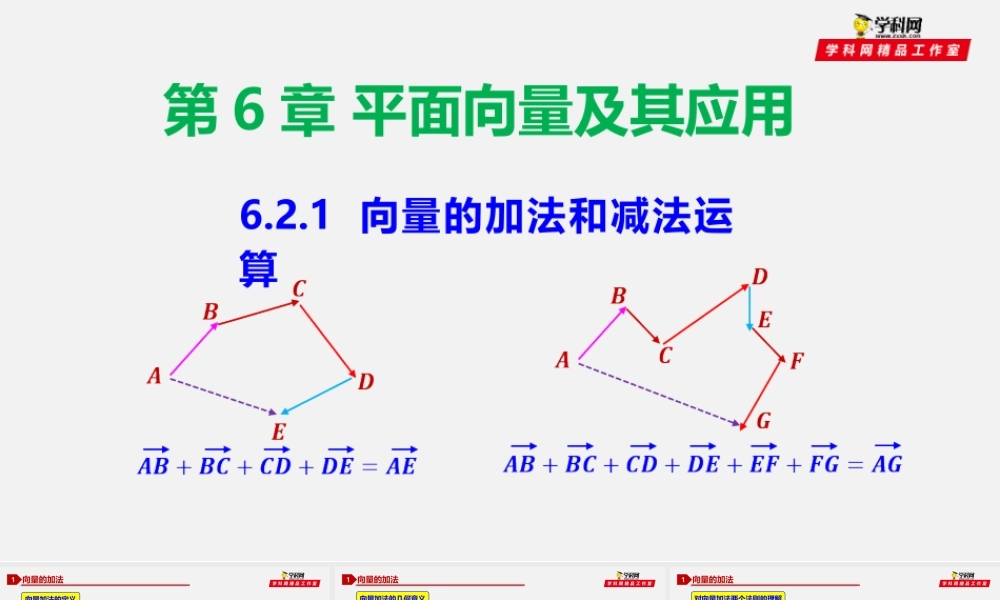
第6章平面向量及其应用6.2.1向量的加法和减法运算向量的加法1向量加法的定义★求两个向量的和的运算,叫做向量的加法;★两个向量的和,仍然是一个向量;★对于零向量和任意向量,规定:向量加法的交换律和结合律【向量加法的交换律】【向量加法的结合律】多个向量的加法运算可以按照任意的次序与任意的组合进行,如:向量的加法1向量加法的几何意义【1】三角形法则:如图,已知非零向量,,在平面内任取一点,作AB=,BC=,则向量AC叫做与的和,记作,即:这种求向量和的方法,叫做向量加法的三角形法则.【2】平行四边形法则:如图,以同一点O为起点的两个已知向量,,以OA,OB为邻边做平行四边形OACB,则以O点为起点的向量OC(OC是对角线)就是相量与的和.我们把这种作两向量的加法1对向量加法两个法则的理解【1】两个法则的使用条件不同:【2】当两个向量不共线时,两个法则是一致的.★三角形法则适用于任意两个非零向量求和★平行四边形法则只适用于两个不共线的相量求和如图所示,AC=AB+AD(平行四边形法则),又因为BC=AD,所以AC=AB+BC(三角形法则)【3】三角形法则中强调“首尾相连”;平行四边形法则中强调的是“共起点,不共线”.【4】作三个或者三个以上的向量求和时,使用三角形法则更简单.向量的加法1高阶笔记拓展【1】在三角形ABC中,AB+BC+CA=0;AB+BC=AC【2】向量求和的多边形法则:已知n个向量,依次首尾连接,则由起始向量的起点,指向末尾向量的终点的向量,即为这些向量的和.这叫做向量求和的多边形法则.向量的减法2与已知向量的模相等,方向相反的向量叫做的相反向量,记作.相反向量向量减法的定义向量加上向量的相反向量,叫做与的差,即★规定:零向量的相反向量还是零向量,即★任意向量与其相反向量的和是零向量,即★如果与互为相反向量,那么向量减法的实质是向量加法的逆运算.利用相反向量的定义,可以把向量的减法转化成向量的加法来计算.向量的减法2作法①:如图,已知非零向量,,在平面内任取一点O,作OA=,OB=,则BA=,即可以表示为从向量的终点指向向量的终点的向量.简记为“共起点,连终点,指被减”向量减法的几何意义作法②:(相反向量法)在平面内任取一点O,作OA=,OB=,OD=,连接AB.由向量减法的定义,可知在四边形OCAB中,OB//CA,且OB=CA,所以四边形OCAB是平行四边形,所以BA=OC=.→→向量的减法2【1】当,反向时,与同向,且盘点三大易错点①若,则,与,都同向,且【2】当,同向时——②若,则,与,都反向,且②...