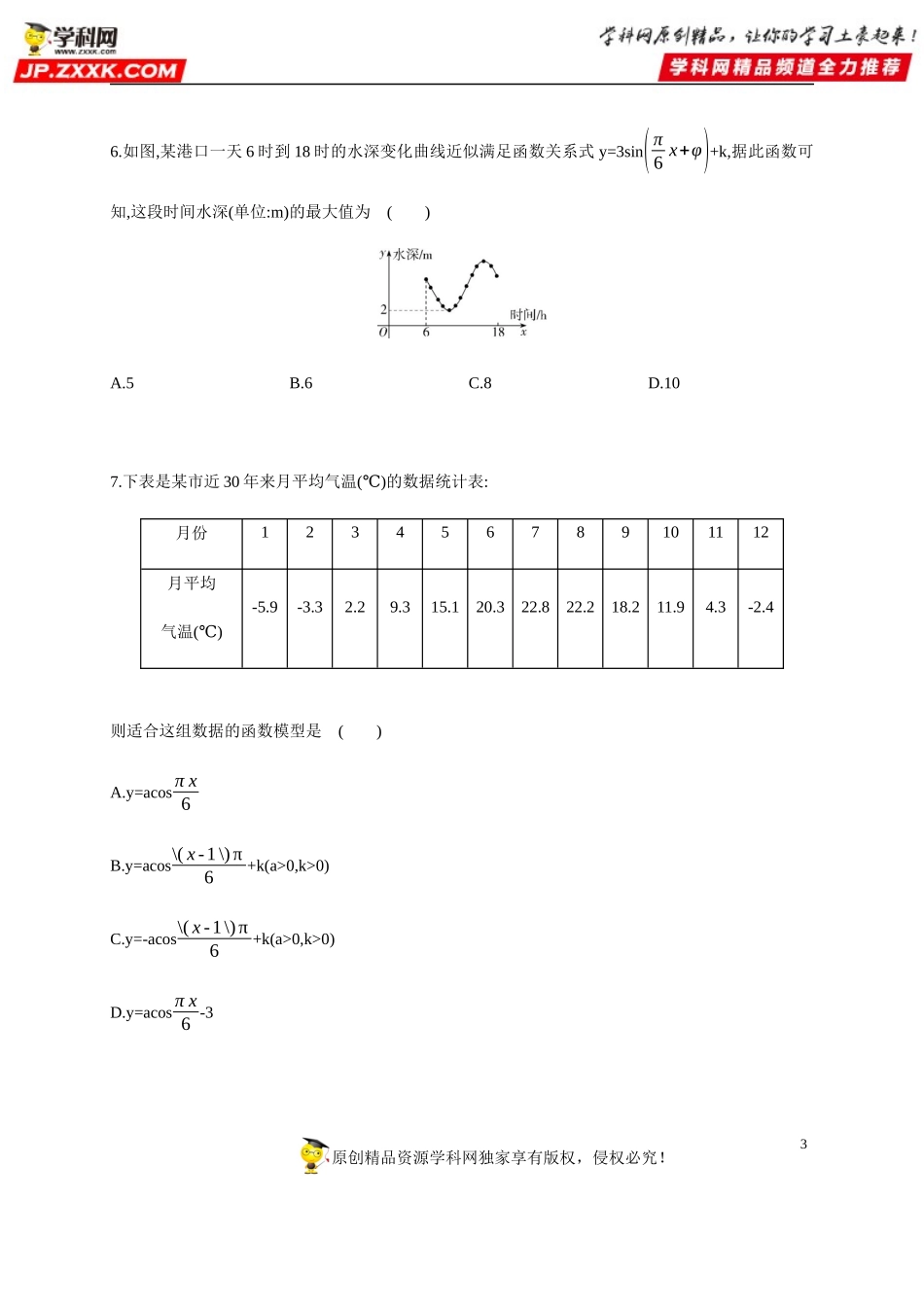
1原创精品资源学科网独家享有版权,侵权必究!第五章三角函数课时5.7三角函数的应用1.了解y=Asin(ωx+φ)的图象的物理意义,能指出简谐运动中的振幅、周期、相位、初相.2.会用三角函数构建物理中周期变化的数学模型.3.能用三角函数模型解决一些具有周期变化规律的实际问题.基础过关练题组一函数式y=Asin(ωx+φ)描述简谐运动时的基本概念1.已知简谐运动f(x)=2sin(π3x+φ)(|φ|<π2)的图象经过点(0,1),则()A.T=6,φ=π6B.T=6,φ=π3C.T=6π,φ=π6D.T=6π,φ=π32.简谐运动y=12sin(π8x−2)的频率f=.2原创精品资源学科网独家享有版权,侵权必究!题组二三角函数模型在物理中的应用3.一根长lcm的线,一端固定,另一端悬挂一个小球,小球摆动时离开平衡位置的位移s(cm)与时间t(s)的函数关系式是s=3cos(❑√glt+π3),其中g是重力加速度,当小球摆动的周期是1s时,线长l等于()A.gπB.g2πC.gπ2D.g4π24.弹簧上挂的小球做上下振动,它在时间t(s)时离开平衡位置的位移s(cm)(假设向上为正)满足函数关系式s=2sin(t+π4).给出下列三种说法:①小球开始时在平衡位置上方❑√2cm处;②小球下降到最低点时在平衡位置下方2cm处;③每经过2πs小球重复振动一次.其中正确的说法是()A.①②B.②③C.①③D.①②③5.如图所示,弹簧下挂着的小球做上下振动.开始时小球在平衡位置上方2cm处,然后小球向上运动,小球的最高点和最低点与平衡位置的距离都是4cm,每经过πs小球往复振动一次,则小球离开平衡位置的位移y(cm)(假设向上为正)与振动时间x(s)的关系式可以是.题组三三角函数模型在生活中的应用3原创精品资源学科网独家享有版权,侵权必究!6.如图,某港口一天6时到18时的水深变化曲线近似满足函数关系式y=3sin(π6x+φ)+k,据此函数可知,这段时间水深(单位:m)的最大值为()A.5B.6C.8D.107.下表是某市近30年来月平均气温()℃的数据统计表:月份123456789101112月平均气温()℃-5.9-3.32.29.315.120.322.822.218.211.94.3-2.4则适合这组数据的函数模型是()A.y=acosπx6B.y=acos\(x-1\)π6+k(a>0,k>0)C.y=-acos\(x-1\)π6+k(a>0,k>0)D.y=acosπx6-34原创精品资源学科网独家享有版权,侵权必究!8.如图所示,质点P在半径为2的圆周上按逆时针方向运动,其初始位置为P0(❑√2,-❑√2),角速度为1rad/s,那么点P到x轴的距离d关于时间t(s)的函数图象大致为()9.国际油价在某一时间内呈现正弦波动规律:P=Asin(ωπt+π4)+60(单位:美元,t为天数,A>0,ω>0),现采集到下列信息:最高油价80美元,当t=150时,...