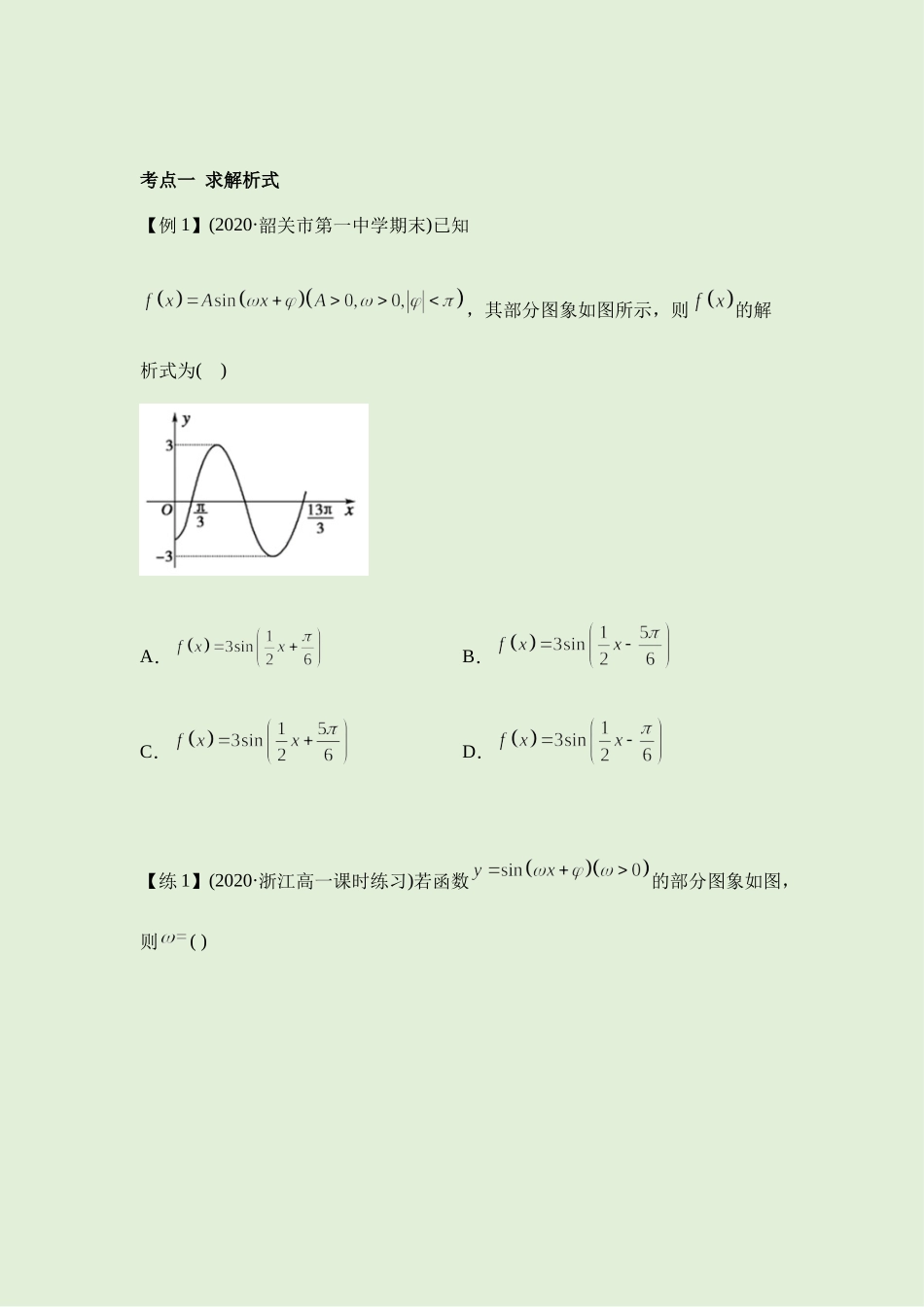
5.6函数y=Asin(ωx+φ)知识点A,ω,φ对函数y=Asin(ωx+φ)图象的影响1.φ对y=sin(x+φ),x∈R图象的影响2.ω(ω>0)对y=sin(ωx+φ)图象的影响3.A(A>0)对y=Asin(ωx+φ)图象的影响考点一求解析式【例1】(2020·韶关市第一中学期末)已知,其部分图象如图所示,则的解析式为()A.B.C.D.【练1】(2020·浙江高一课时练习)若函数的部分图象如图,则()A.B.C.D.考点二伸缩平移【例2】(2020·应城市第一高级中学高一月考)已知函数的最小正周期为,将该函数的图象向左平移个单位后,得到的图象对应的函数为偶函数,则的图象()A.关于点对称B.关于直线对称C.关于点对称D.关于直线对称【练2】(2020·浙江衢州·高一期末)要得到函数的图象,只需将函数的图象()A.向左平移个单位长度B.向右平移个单位长C.向左平移个单位长度D.向右平移个单位长度考点三综合运用【例3】(2020·湖南益阳·高一期末)已知函数的部分图象如图所示.(1)求函数的解析式;(2)将函数的图象向左平移个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变)得到函数的图象,求函数在区间上的值域.【练3】(2020·河南林州一中高一月考)函数的图象向左平移个单位后关于轴对称,则函数在上的最小值为()A.B.C.D.课后练习1.(2021高一下·衢州月考)将函数y=cos2x的图象向右平移π4个单位后,所得函数图象的一条对称轴方程为()A.x=π8B.x=π4C.x=π2D.x=5π82.(2021·桂林模拟)将函数f(x)=12sin(ωx+π6)+2(ω>0)的图像向右平移π3个单位长度后与原函数图像重合,则实数ω的最小值是()A.2B.3C.6D.93.(2020高一上·毕节期末)将函数y=sin(x−π4)的图像上所有点的横坐标变为原来的2倍(纵坐标不变),再将所得的图像向左平移π6个单位,则所得图像对应的解析式为()A.y=sin(2x+π12)B.y=sin(2x−π12)C.y=sin(x2−π6)D.y=sin(x2−π12)4.(2021高二下·梅州期末)若将函数f(x)=sin(2x+π4)的图象向右平移φ个单位,所得图象关于y轴对称,则φ的最小正值是()A.π8B.π4C.3π8D.3π45.(2021高一下·驻马店期末)已知函数f(x)=sin(ωx+φ)(ω>0,φ∈(π2,π))的部分图象如图所示,则f(2021)=¿.6.(2020高一上·芜湖期末)将函数y=sin(2x−π6)的图象向左平移φ后得到一个奇函数的图象,则φ的最小正值是.7.(2020高一上·合肥期末)将函数y=cos(2x−43π)的图象向左平移φ(φ>0)个单位,所得图象关于y轴对称,则φ的最小值为________.8.(2021高二...