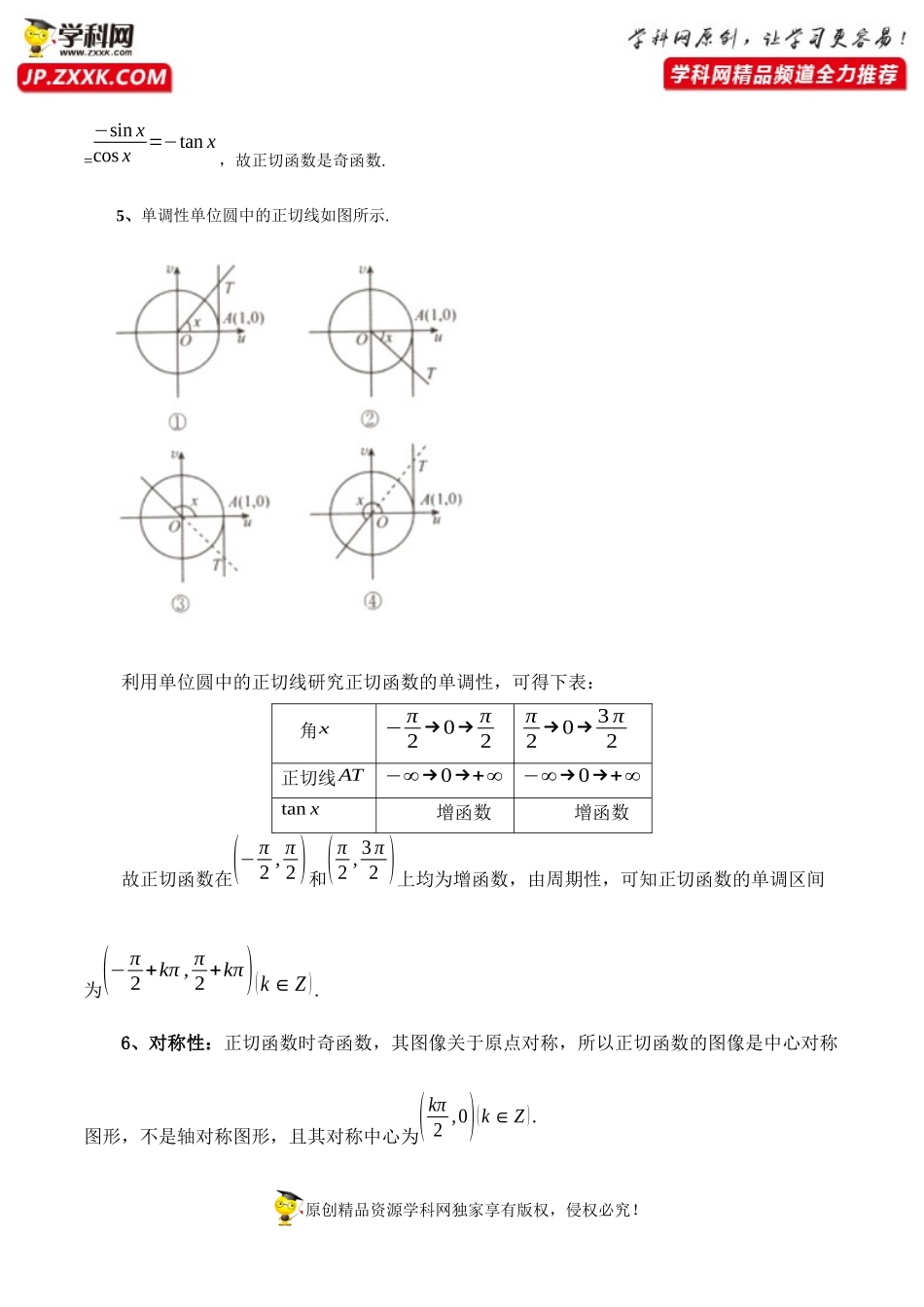
原创精品资源学科网独家享有版权,侵权必究!5.4.3正切函数的性质与图像(基础知识+基本题型)知识点一正切函数的性质1、定义域:{x|x≠π2+kπ,k∈Z}2、值域:R从单位圆上的正切线可知,当x<π2+kπ(k∈Z)且无限接近于π2+kπ时,tanx无限增大,记作tanx→+∞(tanx趋向于正无穷大);当x>π2−kπ(k∈Z)且无限接近于k2时,tanx无限减小,记作tanx→−∞(tanx趋向于负无穷大).因此tanx可以取任何实数值,但没有最大值和最小值.称x=−π2+kπ,k∈Z为正切函数图像的渐近线.3、周期性:由诱导公式可知,tan(x+π)=tanx,x∈R,x≠π2+kπ,k∈Z.因此正切函数是周期函数,周期为π.拓展:函数y=Atan(ωx+ϕ)(A≠0,ω≠0)的最小正周期T=π|ω|.4、奇偶性:正切函数的定义域为{x|x≠π2+kπ,k∈Z},关于原点对称,由于tan(−x)=sin(−x)cos(−x)原创精品资源学科网独家享有版权,侵权必究!=−sinxcosx=−tanx,故正切函数是奇函数.5、单调性单位圆中的正切线如图所示.利用单位圆中的正切线研究正切函数的单调性,可得下表:角x−π2→0→π2π2→0→3π2正切线AT−∞→0→+∞−∞→0→+∞tanx增函数增函数故正切函数在(−π2,π2)和(π2,3π2)上均为增函数,由周期性,可知正切函数的单调区间为(−π2+kπ,π2+kπ)(k∈Z).6、对称性:正切函数时奇函数,其图像关于原点对称,所以正切函数的图像是中心对称图形,不是轴对称图形,且其对称中心为(kπ2,0)(k∈Z).原创精品资源学科网独家享有版权,侵权必究!警示:正切函数y=tanx在(−π2+kπ,π2+kπ)(k∈Z)内是单调递增函数,但不能说函数在其定义域内是单调递增函数.知识点二正切函数的图像类比正弦函数的图像的作法,作正切函数y=tanx,x∈(−π2,π2)的图像的步骤:(1)所示,建立平面直角坐标系,在x轴的负半轴上任取一点O1,以O1为圆心作单位圆.(2)把单位圆中的右半圆平均分成8份,并作出相应终边的正切线.(3)在x轴上,把(−π2,π2)这一段分成8等份,依次确定单位圆上7个分点在x轴上的位置.(4)把角x的正切线向右平移,使它的起点与x轴上的点x重合.(5)用光滑的曲线把正切线的终点连接起来,就得到y=tanx,x∈(−π2,π2)的图像.现在我们作出了正切函数一个周期上的图像,根据正切函数的周期性,把上述的图像向原创精品资源学科网独家享有版权,侵权必究!左、右扩展,就可以得到正切函数y=tanx,x∈R,x≠π2+kπ,k∈Z的图像,我们把它叫做正切曲线(如图1.4—16所示).它是由被无数条直线x=π2...