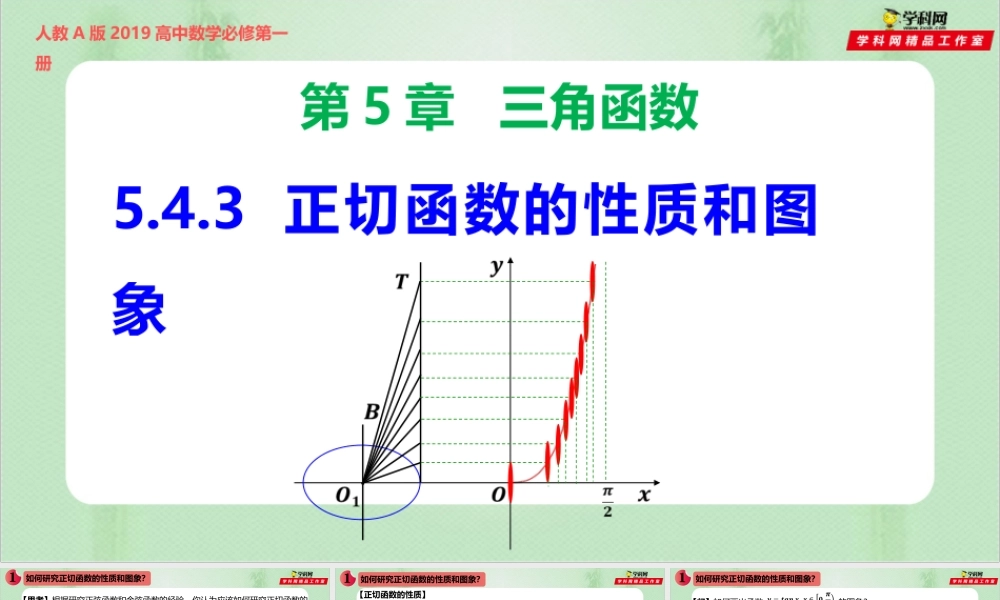
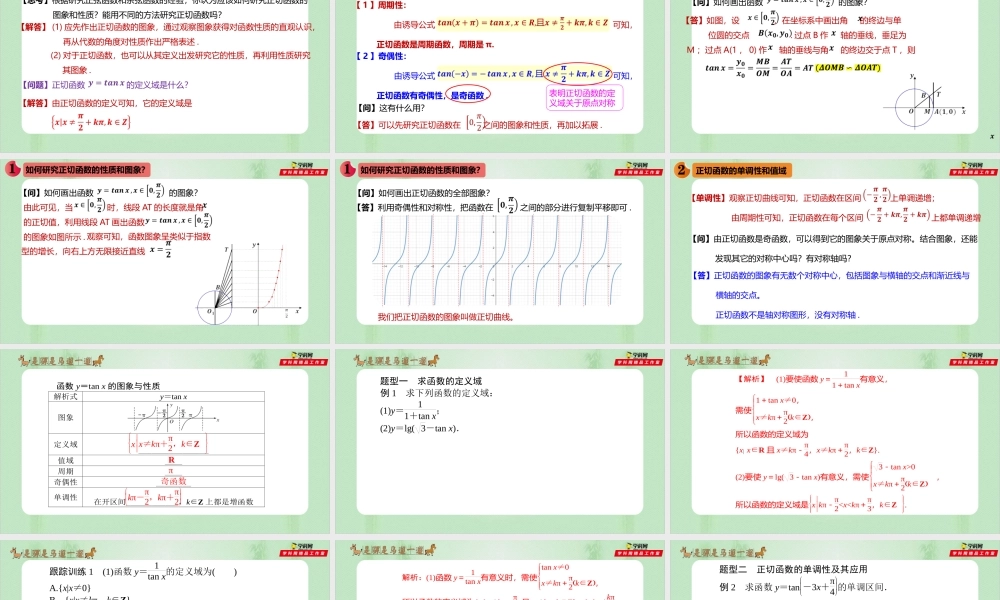
第5章三角函数5.4.3正切函数的性质和图象人教A版2019高中数学必修第一册如何研究正切函数的性质和图象?【思考】根据研究正弦函数和余弦函数的经验,你认为应该如何研究正切函数的图象和性质?能用不同的方法研究正切函数吗?【解答】(1)应先作出正切函数的图象,通过观察图象获得对函数性质的直观认识,再从代数的角度对性质作出严格表述.(2)对于正切函数,也可以从其定义出发研究它的性质,再利用性质研究其图象.【问题】正切函数的定义域是什么?【解答】由正切函数的定义可知,它的定义域是【2】奇偶性:由诱导公式可知,正切函数有奇偶性,是奇函数.【1】周期性:由诱导公式可知,正切函数是周期函数,周期是π.如何研究正切函数的性质和图象?【正切函数的性质】表明正切函数的定义域关于原点对称【问】这有什么用?【答】可以先研究正切函数在之间的图象和性质,再加以拓展.如何研究正切函数的性质和图象?【问】如何画出函数的图象?【答】如图,设,在坐标系中画出角的终边与单位圆的交点.过点B作轴的垂线,垂足为M;过点A(1,0)作轴的垂线与角的终边交于点T,则如何研究正切函数的性质和图象?【问】如何画出函数的图象?由此可见,当时,线段AT的长度就是角的正切值,利用线段AT画出函数的图象如图所示.观察可知,函数图象呈类似于指数型的增长,向右上方无限接近直线如何研究正切函数的性质和图象?【问】如何画出正切函数的全部图象?【答】利用奇偶性和对称性,把函数在之间的部分进行复制平移即可.我们把正切函数的图象叫做正切曲线。正切函数的单调性和值域【单调性】观察正切曲线可知,正切函数在区间上单调递增;由周期性可知,正切函数在每个区间上都单调递增【问】由正切函数是奇函数,可以得到它的图象关于原点对称。结合图象,还能发现其它的对称中心吗?有对称轴吗?【答】正切函数的图象有无数个对称中心,包括图象与横轴的交点和渐近线与横轴的交点。正切函数不是轴对称图形,没有对称轴.函数y=tanx的图象与性质解析式y=tanx图象定义域________________值域____周期____奇偶性________单调性在开区间____________,k∈Z上都是增函数xx≠kπ+π2,k∈ZRπ奇函数kπ-π2,kπ+π2题型一求函数的定义域例1求下列函数的定义域:(1)y=11+tanx;(2)y=lg(3-tanx).【解析】(1)要使函数y=11+tanx有意义,需使1+tanx≠0,x≠kπ+π2k∈Z,所以函数的定义域为{xx∈R且x≠...