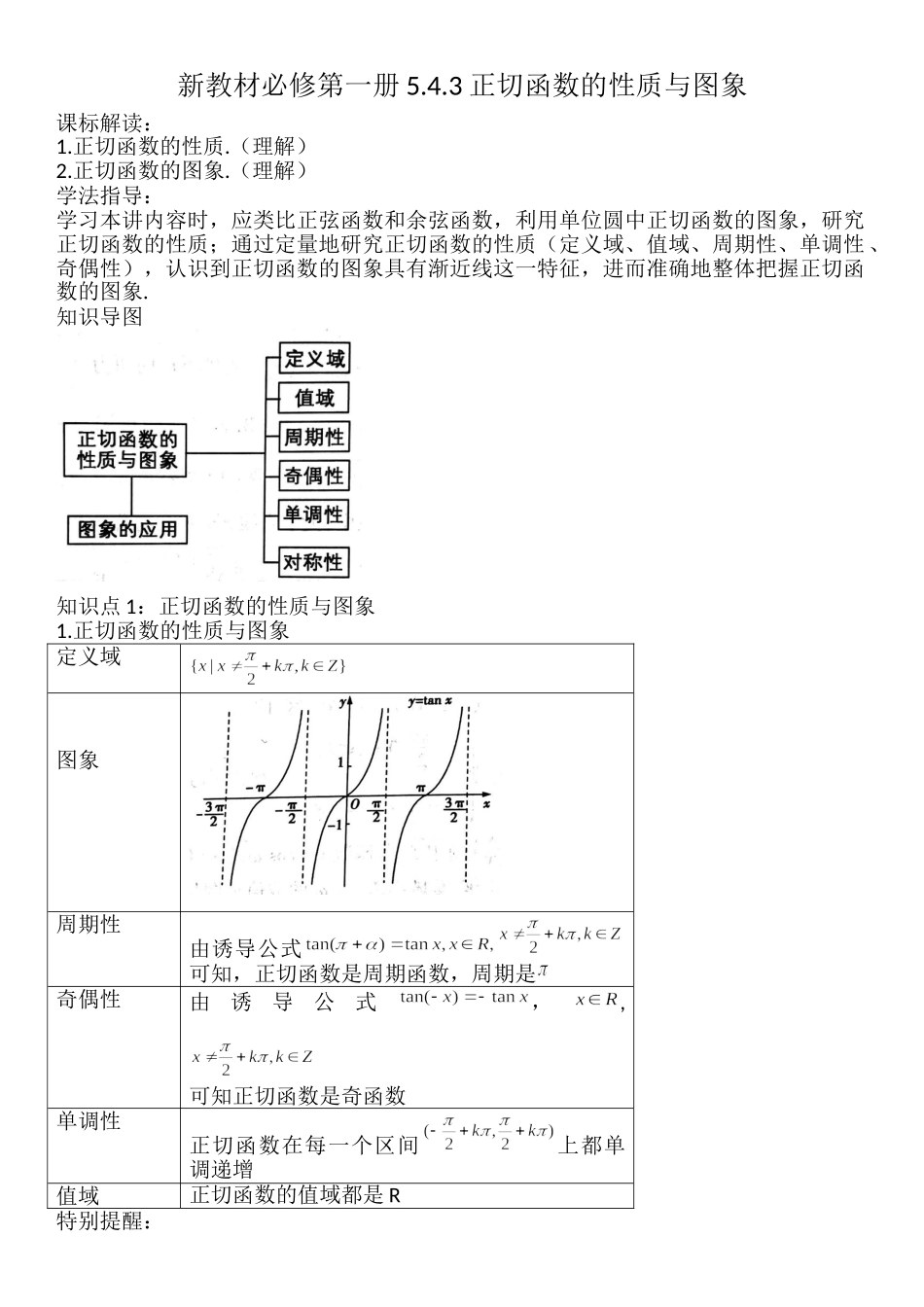
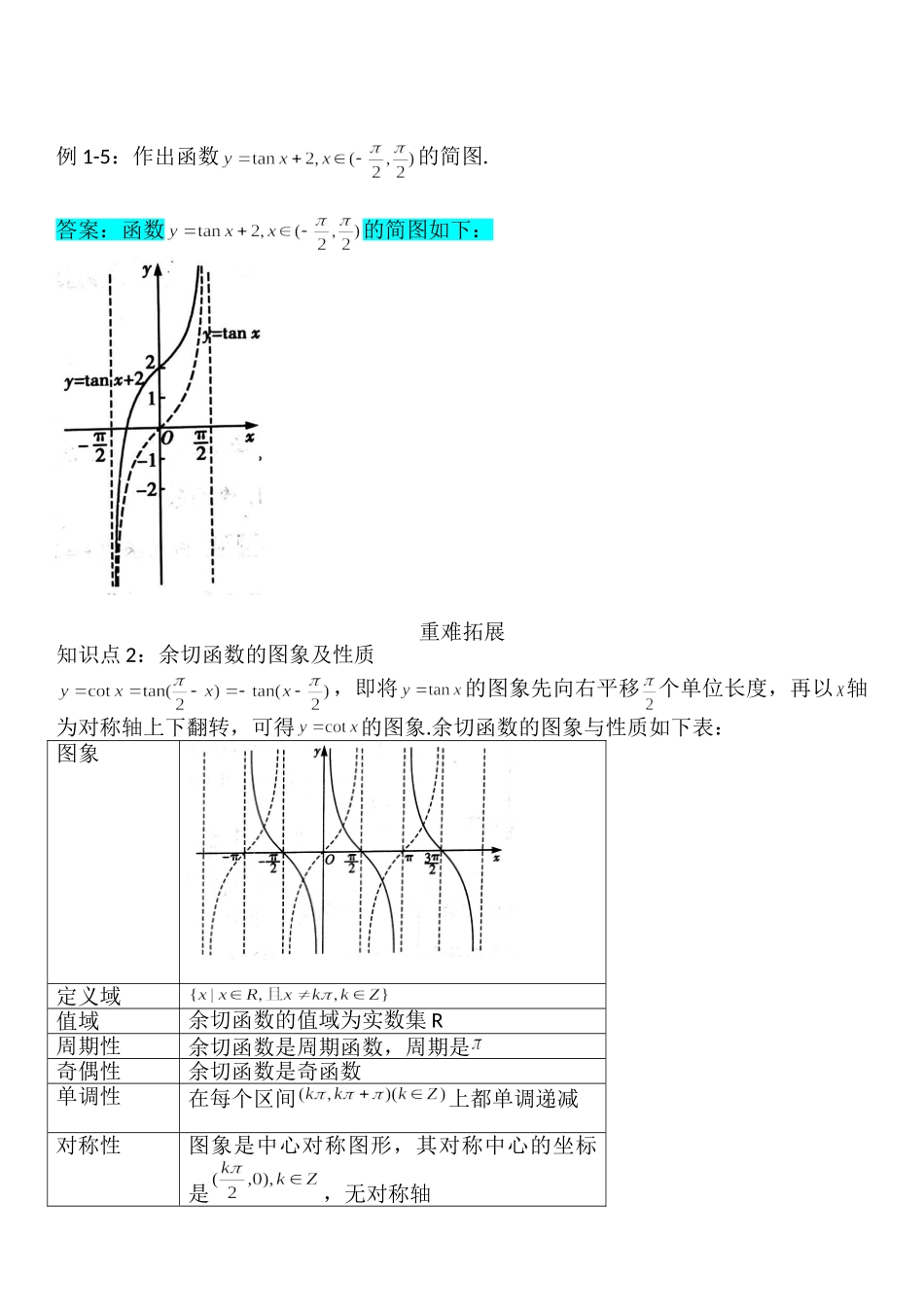
新教材必修第一册5.4.3正切函数的性质与图象课标解读:1.正切函数的性质.(理解)2.正切函数的图象.(理解)学法指导:学习本讲内容时,应类比正弦函数和余弦函数,利用单位圆中正切函数的图象,研究正切函数的性质;通过定量地研究正切函数的性质(定义域、值域、周期性、单调性、奇偶性),认识到正切函数的图象具有渐近线这一特征,进而准确地整体把握正切函数的图象.知识导图知识点1:正切函数的性质与图象1.正切函数的性质与图象定义域图象周期性由诱导公式可知,正切函数是周期函数,周期是奇偶性由诱导公式,,可知正切函数是奇函数单调性正切函数在每一个区间上都单调递增值域正切函数的值域都是R特别提醒:(1)正切函数在定义域上不具备单调性,因此不能说函数在其定义域上是单调递增函数.(2)正切函数无单调递减区间,在每一个单调区间上都是单调递增的,并且每个单调区间都是开区间.(3)正切函数没有最大值和最小值.(4)正切型函数的最小正周期为.例1-1:函数的定义域为.答案:例1-2:函数的值域为.答案:[-1,1]例1-3:若,则()A.B.C.D.答案:D2.利用奇偶性和周期性画出正切曲线的具体步骤如下左图所示,设,在平面直角坐标系中画出角的终边与单位圆的交点B().过点B作轴的垂线,垂足为M;过点A(1,0)作轴的垂线与角的终边交于点T,则由此可见,当时,线段AT的长度就是相应角的正切值.我们可以利用线段AT画出函数,的图象如上右图所示.3.三点两线法作正切曲线简图类比正、余弦函数图象的五点法,我们可以采用三点法作正切函数的简图.“三点”是指点;“两线”是指直线和.在三点两线确定的情况下,可以大致画出正切函数在区间上的简图.例1-4:画出函数的图象,并根据图象判断其单调区间和奇偶性.答案:函数的图象如图所示:例1-5:作出函数的简图.答案:函数的简图如下:重难拓展知识点2:余切函数的图象及性质,即将的图象先向右平移个单位长度,再以轴为对称轴上下翻转,可得的图象.余切函数的图象与性质如下表:图象定义域值域余切函数的值域为实数集R周期性余切函数是周期函数,周期是奇偶性余切函数是奇函数单调性在每个区间上都单调递减对称性图象是中心对称图形,其对称中心的坐标是,无对称轴例2-6:求函数的单调区间.答案:单调增区间是,无单调递减区间.例2-7:比较与的大小.答案:>题型与方法题型1:正切函数图象的应用1.作图象例8:画出函数在上的简图.参考答案:2.图象识别问题例9:(1)如图中的图形分别是①②③④...