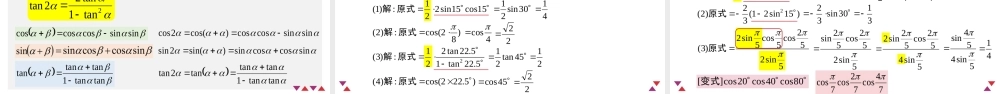5.5 三角恒等变换(含2课时)-2022-2023学年高一数学教材配套教学精品课件（人教A版2019必修第一册).pptxVIP免费

5.5三角恒等变换5.5.1两角和与差的正弦、余弦和正切公式温故而知新三角函数的两种定义（1）若角α的终边与单位圆(半径为1)的交点坐标为(x,y)，则sinα=_____，cosα=_____，tanα=_____.（2）若角α的终边上任一点坐标为(x,y),则sinα=_____，cosα=_____，tanα=_____.其中r=__________.如：若角θ的终边过点(12﹣，5)，则sinθ=_____，cosθ=_____，tanθ=_____.tan)tan(cos)cos(sin)sin(tan)tan(cos)cos(sin)sin(tan)tan(cos)cos(sin)sin(tan)2tan(cos)2cos(sin)2sin(kkksin)2cos(cos)2sin(sin)2cos(cos)2sin(316sin32sin)3sin(3sin23温故而知新316sin或34sin)3sin(3sin23三角恒等变换小化锐大化小负化正探究1：cos(α－β)与角α、β的正余弦间的关系α的终边k2不妨设)(的终边不重合与β的终边α－β的终边AO1AP1P))sin(),(cos(P)sin,(cos1A)sin,(cos1P,11得由PAAP)(sin]1)[cos(22)0,1(A22)sin(sin)cos(cos,化简得sinsincoscos)cos(:)(C差角的余弦公式结论：两角和与差的余弦公式sinsincoscos)cos(:)(C)](cos[()cos()sin(sin)cos(cossinsincoscossinsincoscos)cos(:)(C推导：15cos)3045cos(30sin45sin30cos45cos4262122232242622232221)4560cos(45sin60sin45cos60cosP217-2运用：两角和与差的余弦公式.______,4),3,2(为与单位圆的交点横坐标的终边角后的终边顺时针旋转将的终边过点已知角,132cos,2133sin:已知析)4cos('cos旋转后4sinsin4coscos26261322)133132(22探究2：sin(α±β)与cos(α±β)的关系sinsincoscos)cos(sinsincoscos)cos()(2cos)sin()(2cos)sin()2(cossin)2sin(cos)2cos(sincoscossin...