5.3.2 对数的运算（课件）-【中职专用】高一数学同步精品课堂（高教版2021·基础模块下）.pptxVIP免费

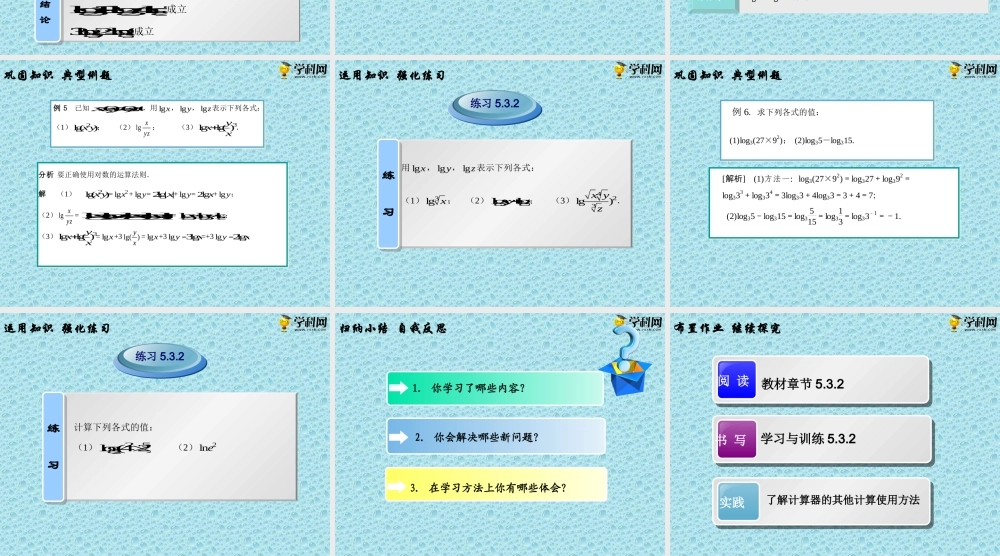
5.3.2对数的运算第五章指数函数与对数函数当0,1,0Naa时，NabbNalog底底指数对数幂真数回顾知识复习导入对数性质（1）log10a；（2）log1aa；（3）N>0，即零和负数没有对数．常用对数：以10为底的对数N10logNlg简记为以e为底的对数自然对数：elogNNln简记为回顾知识复习导入创设情景兴趣导入20世纪30年代，美国加州理工学院的地震学家里克特和古登堡提出了一种地震震级标度，以发生地震时产生的水平位移作为判断标准，即目前通用的里氏震级，震级每增加一级，通过地震释放的能量增加约32倍，里氏震级的计算公式为0lglgMAA，其中A表示地震的最大振幅，A0表示“标准地震”的振幅，里氏震级的计算公式涉及对数运算的哪些运算法则？创设问题自我探究计算器问题问题用计算器验证等式lg2lg5=lg7、lg2lg5=lg10是否成立？等式222log12log4log8、222log12log4log3是否成立？等式333log2log6、333log2log8是否成立？结论结论lg2lg5=lg10成立222log12log4log3成立333log2log8成立动脑思考探索新知动脑思考探索新知对数运算法则对数运算法则法则1lglglgMNMN（M>0，N>0）法则2lglglgMMNN（M>0，N>0）法则3lgnM=nlgM（n为整数，M>0）巩固知识典型例题例5已知0,0,0xyz，用lgx，lgy，lgz表示下列各式：（1）2lg()xy；（2）lgxyz；（3）3lglg()yxx．分析要正确使用对数的运算法则．解（1）2lg()xy=2lgx+lgy=2lg||x+lgy=2lgx+lgy；（2）lgxyz=lglglglglgxyzxyz（）=lglglgxyz；（3）3lglg()yxx=lgx+3lg()yx=lgx+3lgy3lgx=+3lgy2lgx运用知识强化练习练习5.3.2练习练习用lgx，lgy，lgz表示下列各式：（1）3lgx；（2）lglgxyz；（3）423lg)xyz．巩固知识典型例题例6．求下列各式的值：(1)log3(27×92)；(2)log35－log315.[解析](1)方法一：log3(27×92)＝log327＋log392＝log333＋log334＝3log33＋4log33＝3＋4＝7；(2)log35－log315＝log3515＝log313＝log33－1＝－1.运用知识强化练习练习5.3.2练习练习计算下列各式的值：（1）252log(42)（2）2lne3.在学习方法上你有哪些体会？2.你会解决哪些新问题？1.你学习了哪些内容？归纳小结自我反思阅读教材章节5.3.2书写学习与训练5.3.2布置作业继续探究实践了解计算器的其他计算使用方法