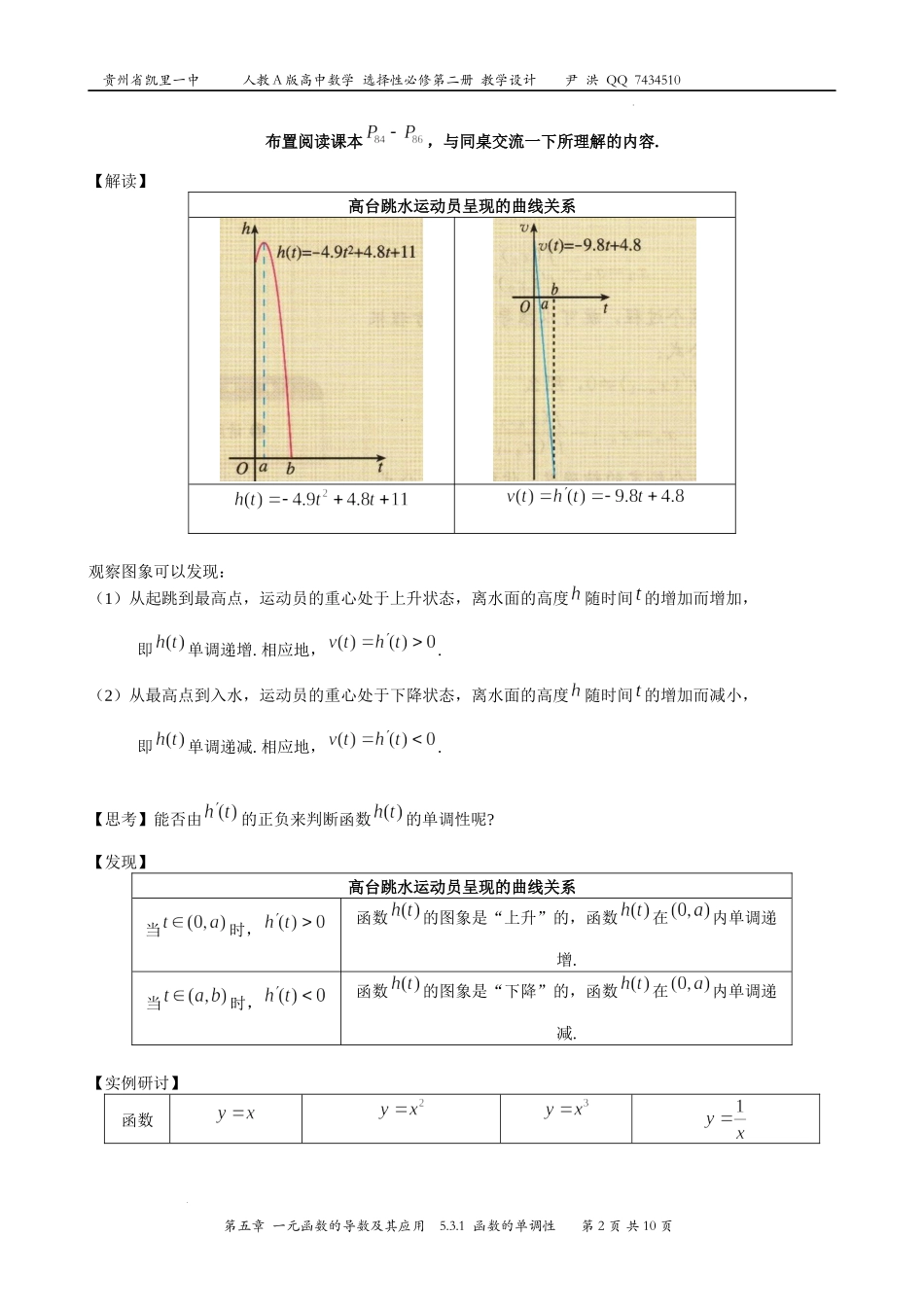
贵州省凯里一中人教A版高中数学选择性必修第二册教学设计尹洪QQ7434510第五章一元函数的导数及其应用5.3.1函数的单调性第1页共10页学科网(北京)股份有限公司第五章一元函数的导数及其应用5.3导数在研究函数中的应用5.3.1函数的单调性一、教学目标1、通过函数的单调性与导数的正负之间的关系得出利用导数判断函数单调性的方法.2、熟练掌握利用导数判断函数单调性的方法.二、教学重点、难点重点:利用导数判断函数的单调性.难点:熟练应用导数解决函数单调性的问题.三、学法与教学用具1、学法:学生在老师的引导下,通过阅读教材,自主学习、思考、交流、讨论和概括,从而完成本节课的教学目标.2、教学用具:多媒体设备等四、教学过程(一)创设情景,揭示课题【回顾】导数的几何意义与切线方程函数在处的切线的斜率过点的切线方程【思考】导数的应用只能是解决切线的问题吗?【情景】过山车呈现的曲线过山车是一项富有刺激性的娱乐工具.那种风驰电掣、有惊无险的快感令不少人着迷.【问题】过山车在设计过程中用到了那些数学知识呢?(二)阅读精要,研讨新知贵州省凯里一中人教A版高中数学选择性必修第二册教学设计尹洪QQ7434510第五章一元函数的导数及其应用5.3.1函数的单调性第2页共10页学科网(北京)股份有限公司布置阅读课本,与同桌交流一下所理解的内容.【解读】高台跳水运动员呈现的曲线关系观察图象可以发现:(1)从起跳到最高点,运动员的重心处于上升状态,离水面的高度随时间的增加而增加,即单调递增.相应地,.(2)从最高点到入水,运动员的重心处于下降状态,离水面的高度随时间的增加而减小,即单调递减.相应地,.【思考】能否由的正负来判断函数的单调性呢?【发现】高台跳水运动员呈现的曲线关系当时,函数的图象是“上升”的,函数在内单调递增.当时,函数的图象是“下降”的,函数在内单调递减.【实例研讨】函数贵州省凯里一中人教A版高中数学选择性必修第二册教学设计尹洪QQ7434510第五章一元函数的导数及其应用5.3.1函数的单调性第3页共10页学科网(北京)股份有限公司图象导数的正负单调性在上单调递增在上单调递减,在上单调递增在上单调递增在上单调递减,在上单调递减【函数的单调性与导数的关系】一般地,函数的单调性与导函数的正负之间具有如下的关系:在某个区间上,如果,那么函数在区间上单调递增;在某个区间上,如果,那么函数在区间上单调递减.【例题研讨】阅读领悟课本例1、例2(用时约为2-3分钟,教师作出准...