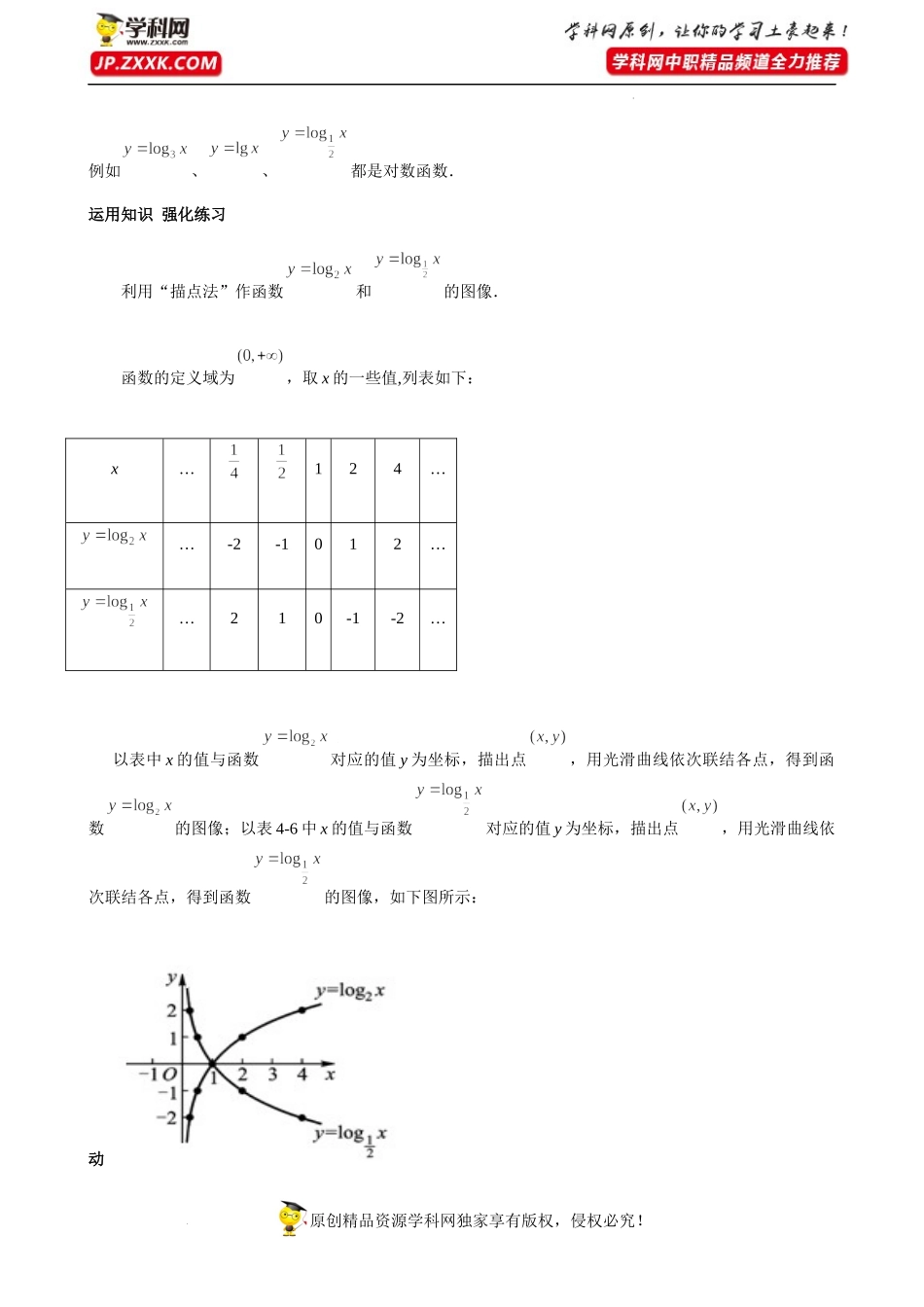
原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司5.4对数函数【教学目标】知识目标:(1)了解对数函数的图像及性质特征;(2)了解对数函数的实际应用.能力目标:(1)观察对数函数的图像,总结对数函数的性质,培养观察能力;(2)通过应用实例的介绍,培养学生数学思维能力和分析与解决问题能力.情感目标:(1)体味对数函数的认知过程,树立严谨的思维习惯;(2)参与数学建模过程,感受生活中的数学模型,体会数学知识的应用;(3)经历合作学习的过程,树立团队合作意识.【教学重点】对数函数的图像及性质.【教学难点】对数函数的应用中实际问题的题意分析.【教学设计】⑴实例引入知识,提升学生的求知欲;⑵“描点法”作图与软件的应用相结合,有助于观察得到指数函数的性质;⑶知识的巩固与练习,培养学生的思维能力;⑷实际问题的解决,培养学生分析与解决问题能力;⑸小组的形式进行讨论、探究、交流,培养团队精神.【教学备品】原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司教学课件.【课时安排】2课时.(90分钟)【教学过程】揭示课题5.4对数函数.创设情景兴趣导入问题学习指数函数时,讨论过细胞的分裂问题:已知某种物质细胞分裂时,得到的细胞个数y是分裂次数x的函数,这个函数表示为,反过来,如果我们知道分裂得到的细胞个数如何求得分裂次数呢?解决由于细胞个数y是分裂次数x的函数,这个函数表示为,由对数的定义可知,分裂次数x与细胞个数y之间关系可以表示为,因为我们习惯用表示自变量,y表示函数,因此将这个函数写成,则x与y的函数关系是,写成对数式为,此时自变量x位于真数位置.动脑思考探索新知概念一般地,形如的函数叫以为底的对数函数,其中a>0且a≠1.“由零和负数和没有对数”可知,对数函数的定义域为,值域为(-∞,+∞).原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司例如、、都是对数函数.运用知识强化练习利用“描点法”作函数和的图像.函数的定义域为,取x的一些值,列表如下:以表中x的值与函数对应的值y为坐标,描出点,用光滑曲线依次联结各点,得到函数的图像;以表4-6中x的值与函数对应的值y为坐标,描出点,用光滑曲线依次联结各点,得到函数的图像,如下图所示:动x…124……-2-1012……210-1-2…原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司脑思考探索新知a>10<a<1图象性质定义域(0,+...