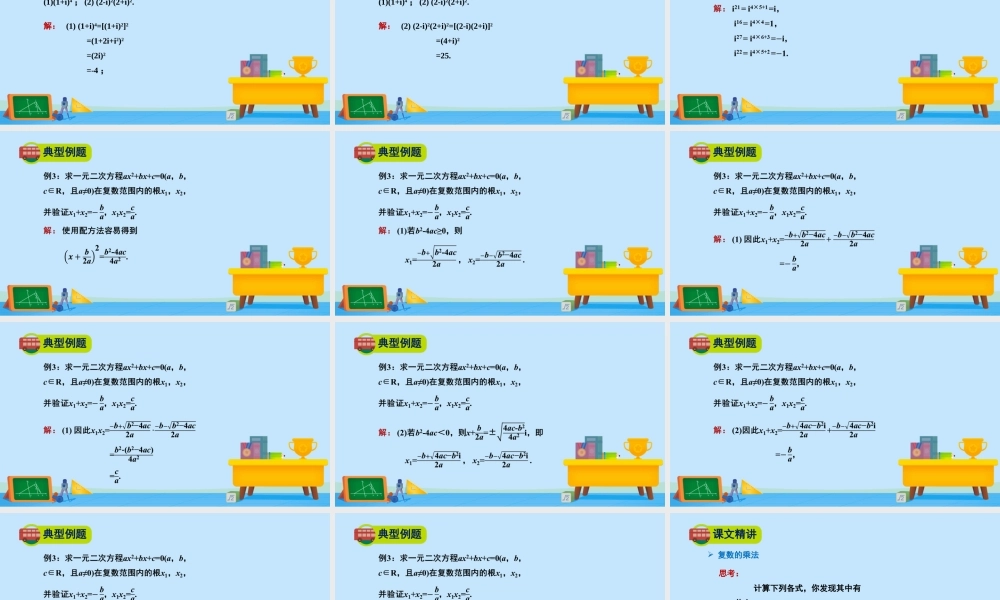
复数的乘法与除法授课教师:温故知新复数的四则运算复数的加法与减法复数加法的几何意义学习目标掌握复数乘法与除法的运算法则,并能熟练地进行乘、除法的运算.(重点、难点)课文精讲复数的乘法对任意两个复数a+bi和c+di(a,b,c,dR)∈,类比多项式乘法,并利用i2=-1,有(a+bi)(c+di)=ac+adi+bci+bdi2=(ac-bd)+(ad+bc)i.因此,定义复数的乘法如下:(a+bi)(c+di)=(ac-bd)+(ad+bc)i课文精讲复数的乘法在进行复数乘法运算时,实际上不直接使用乘法法则,而使用多项式乘法法则.(a+bi)(c+di)=(ac-bd)+(ad+bc)i典型例题例1:计算:(-2-i)(3+i).解:(-2-i)(3+i)=-2×3-2×i-3×i-i×i=-6-2i-3i-i2=-6-2i-3i-1=-5-5i.典型例题课文精讲可以验证,复数的乘法满足交换律、结合律及乘法对加法的分配律,即对任意z1,z2,z3C∈,有复数的乘法(1)交换律:z1·z2=z2·z1;(2)结合律:(z1·z2)·z3=z1·(z2z3);(3)乘法对加法的分配律:z1·(z2+z3)=z1·z2+z1·z3.课文精讲对于复数z,定义它的乘方zn=z·z·····z.根据复数的乘法zm·zn=zm+n,(zm)n=zmn,(z1·z2)n=z1n.·z2n.n个乘法的运算律,实数范围内正整数指数幂的运算性质在复数范围内仍然成立,即对复数z,z1,z2和正整数m,n,有课文精讲复数的乘法在复数的乘方运算中,经常要计算i的乘方,i的乘方有如下规律:一般地,对任意自然数n,有典型例题例1:计算:(1)(1+i)4;(2)(2-i)2(2+i)2.解:(1)(1+i)4=[(1+i)2]2=(1+2i+i2)2=(2i)2=-4;典型例题例1:计算:(1)(1+i)4;(2)(2-i)2(2+i)2.解:(2)(2-i)2(2+i)2=[(2-i)(2+i)]2=(4+i)2=25.典型例题例2:计算:i21,i16,i27,i22.典型例题典型例题典型例题典型例题典型例题典型例题典型例题典型例题课文精讲思考:计算下列各式,你发现其中有什么规律吗?复数的乘法解:(1)(3+2i)(3-2i)=9+4=13;(2)(2+i)(2-i)=4+1=5;课文精讲思考:计算下列各式,你发现其中有什么规律吗?复数的乘法课文精讲复数的乘法典型例题例4:证明:对任意的两个复数,若,则至少有一个为0.课文精讲复数的除法课文精讲设z2=c+di≠0和z=x+yi(c,d,x,y∈R),则z2·z=(c+di)(x+yi)=cx-dy+(cy+dx)i=1,复数的除法所以cx-dy=1,cy+dx=0,解得课文精讲复数的除法课文精讲复数的除法由此可见,在进行复数除法运算时,实际上是将分母“实数化”.典型例题典型例题综合练习已知复数z满足z(1-i)=-2i,则复数z的模为________.综合练习本课小结复数的乘法与除法复数的乘法复数的除法再见