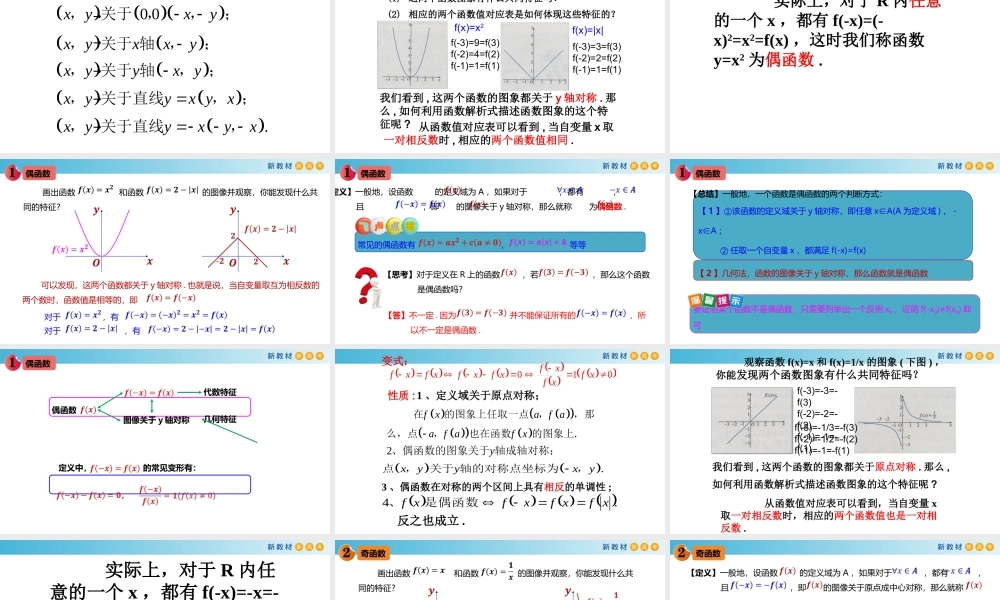
2020沪教版新教材第5章函数的概念、性质及应用5.2.1函数的奇偶性直角坐标平面内的五种对称性:00.xyxyxyxxyxyyxyxyyxyxxyyxyx�����,关于,,;,关于轴,;,关于轴,;,关于直线,;,关于直线,观察下图,思考并讨论以下问题:(1)这两个函数图象有什么共同特征吗?(2)相应的两个函数值对应表是如何体现这些特征的?f(-3)=9=f(3)f(-2)=4=f(2)f(-1)=1=f(1)f(-3)=3=f(3)f(-2)=2=f(2)f(-1)=1=f(1)f(x)=x2f(x)=|x|我们看到,这两个函数的图象都关于y轴对称.那么,如何利用函数解析式描述函数图象的这个特征呢?从函数值对应表可以看到,当自变量x取一对相反数时,相应的两个函数值相同.实际上,对于R内任意的一个x,都有f(-x)=(-x)2=x2=f(x),这时我们称函数y=x2为偶函数.偶函数画出函数和函数的图像并观察,你能发现什么共同的特征?可以发现,这两个函数都关于y轴对称.也就是说,当自变量取互为相反数的两个数时,函数值是相等的,即对于,有对于,有常见的偶函数有,等等偶函数定义】一般地,设函数的定义域为A,如果对于,都有,且,即的图像关于y轴对称,那么就称为偶函数.【思考】对于定义在R上的函数,若,那么这个函数是偶函数吗?【答】不一定.因为并不能保证所有的,所以不一定是偶函数.要证明某个函数不是偶函数,只需要列举出一个反例x0,证明f(-x0)≠f(x0)即可【1】①该函数的定义域关于y轴对称,即任意x∈A(A为定义域),-x∈A;②任取一个自变量x,都满足f(-x)=f(x)偶函数【总结】一般地,一个函数是偶函数的两个判断方式:【2】几何法,函数的图像关于y轴对称,那么函数就是偶函数偶函数偶函数图像关于y轴对称代数特征几何特征定义中,的常见变形有:010xfxfxfxfxfxfxffxafaafafx在的图象上任取一点,,那么,点,也在函数的图象上.2y、偶函数的图象关于轴成轴对称;性质:1、定义域关于原点对称;变式:反之也成立..4xfxfxfxf是偶函数、.xyyxy点,关于轴的对称点坐标为,3、偶函数在对称的两个区间上具有相反的单调性;观察函数f(x)=x和f(x)=1/x的图象(下图),你能发现两个函数图象有什么共同特征吗?f(-3)=-3=-f(3)f(-2)=-2=-f(2)f(-1)=-1=-f(1)f(-3)=-1/3=-f(3)f(-2)=-1/2=-f(2)f(-1)=-1=-f(1)我们看到,这两个函数的图象都关于原点对称.那么,如...