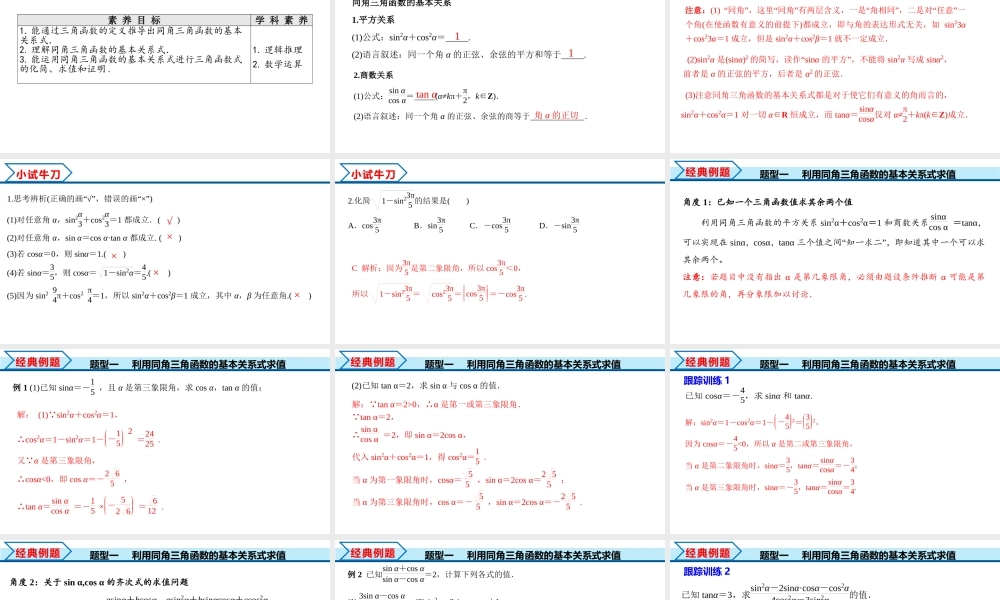
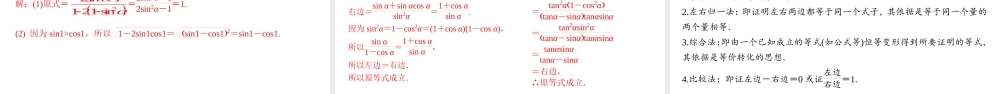5.2.2同角三角函数的基本关系学习目标素养目标学科素养1.能通过三角函数的定义推导出同角三角函数的基本关系式.2.理解同角三角函数的基本关系式.3.能运用同角三角函数的基本关系式进行三角函数式的化简、求值和证明.1.逻辑推理2.数学运算同角三角函数的基本关系1.平方关系(1)公式:sin2α+cos2α=.(2)语言叙述:同一个角α的正弦、余弦的平方和等于.自主学习2.商数关系(1)公式:sinαcosα=(α≠kπ+π2,k∈Z).(2)语言叙述:同一个角α的正弦、余弦的商等于.1tanα角α的正切1自主学习注意:(1)“同角”,这里“同角”有两层含义,一是“角相同”,二是对“任意”一个角(在使函数有意义的前提下)都成立,即与角的表达形式无关,如sin23α+cos23α=1成立,但是sin2α+cos2β=1就不一定成立.(2)sin2α是(sinα)2的简写,读作“sinα的平方”,不能将sin2α写成sinα2,前者是α的正弦的平方,后者是α2的正弦.(3)注意同角三角函数的基本关系式都是对于使它们有意义的角而言的,sin2α+cos2α=1对一切α∈R恒成立,而tanα=sinαcosα仅对α≠π2+kπ(k∈Z)成立.1.思考辨析(正确的画“√”,错误的画“×”)(1)对任意角α,sin2α3+cos2α3=1都成立.()(2)对任意角α,sinα=cosα·tanα都成立.()(3)若cosα=0,则sinα=1.()(4)若sinα=35,则cosα=1-sin2α=45.()(5)因为sin294π+cos2π4=1,所以sin2α+cos2β=1成立,其中α,β为任意角.()×√×小试牛刀××2.化简1-sin23π5的结果是()A.cos3π5B.sin3π5C.-cos3π5D.-sin3π5小试牛刀C解析:因为3π5是第二象限角,所以cos3π5<0,所以1-sin23π5=cos23π5=cos3π5=-cos3π5.题型一利用同角三角函数的基本关系式求值角度1:已知一个三角函数值求其余两个值利用同角三角函数的平方关系sin2α+cos2α=1和商数关系sinαcosα=tanα,可以实现在sinα,cosα,tanα三个值之间“知一求二”,即知道其中一个可以求其余两个。注意:若题目中没有指出α是第几象限角,必须由题设条件推断α可能是第几象限的角,再分象限加以讨论.经典例题题型一利用同角三角函数的基本关系式求值例1(1)已知sinα=-15,且α是第三象限角,求cosα,tanα的值;经典例题解:(1) sin2α+cos2α=1,∴cos2α=1-sin2α=1--152=2425.又 α是第三象限角,∴cosα<0,即cosα=-265,∴tanα=sinαcosα=-15×-526=6...