5.2 三角函数的概念(含2课时)-2022-2023学年高一数学教材配套教学精品课件（人教A版2019必修第一册).pptxVIP免费

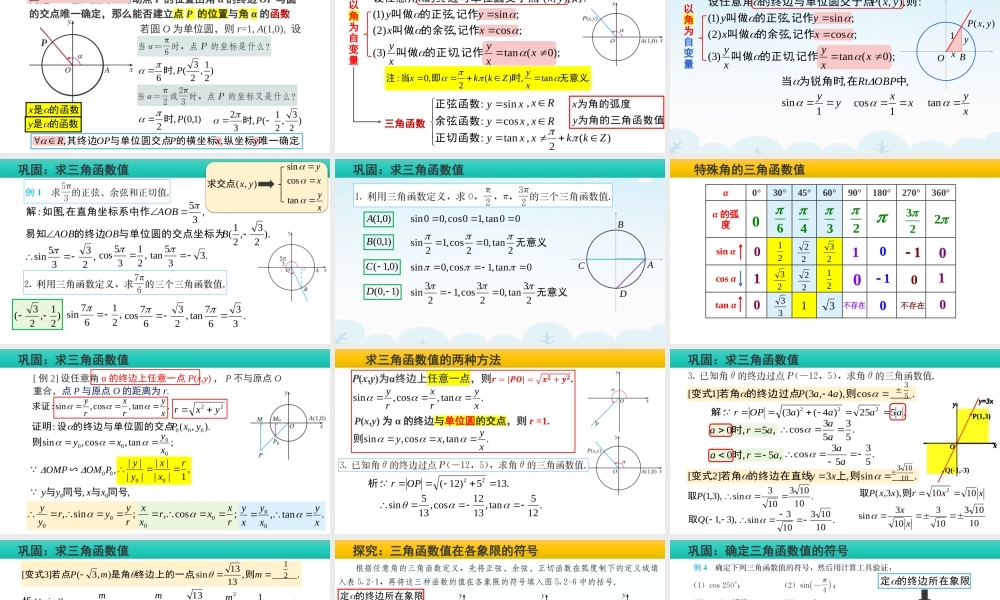
《第五章三角函数》5.2.1三角函数的概念问题1：已知圆周上的动点P的位置由角α的终边OP与圆的交点唯一确定，那么能否建立点P的位置与角α的函数关系？P单位圆：半径为1的圆若圆O为单位圆，则r=1,A(1,0),设P(x,y))21,23(,6P时)1,0(,2P时)23,21(,32P时.,,唯一确定纵坐标的横坐标与单位圆交点其终边yxPOPR的函数是x的函数是y新知1：三角函数的定义:),,(则的终边与单位圆交于点设任意角yxP;sin,)1(yy记作的正弦叫做;cos,)2(xx记作的余弦叫做);0(tan,)3(xxyxy记作的正切叫做.tan,)(2,0:无意义时即当注xyZkkx以角为自变量xyxyxytan:cos:sin:正切函数余弦函数正弦函数三角函数Rx,Rx,)(2,Zkkx为角的三角函数值为角的弧度yx思考：三角函数定义的合理性和统一性:),,(则的终边与单位圆交于点设任意角yxP;sin,)1(yy记作的正弦叫做;cos,)2(xx记作的余弦叫做);0(tan,)3(xxyxy记作的正切叫做以角为自变量),(yxP,,中在为锐角时当OBPRtBxyyy1sinxx1cosxytanO1巩固：求三角函数值,35,,:AOB作在直角坐标系中如图解).23,21(BOBAOB与单位圆的交点坐标为的终边易知,2335sin,2135cos.335tan),(yx求交点xyxytancossin,2167sin,2367cos.3367tan)21,23(巩固：求三角函数值A)0,1(A00tan,10cos,00sinB)1,0(B无意义2tan,02cos,12sinC)0,1(C0tan,1cos,0sin)1,0(D无意义23tan,023cos,123sinD特殊角的三角函数值α0°30°45°60°90°180°270°360°α的弧度sinαcosαtanα23220000000011111不存在不存在03462123332222123213.tan,cos,sin:xyrxry求证,1||||||||00rxxyy巩固：求三角函数值[例2]设任意角α的终边上任意一点P(x,y)，P不与原点O重合，点P与原点O的距离为r.).,(:000yxP的终边与单位圆的交点设证明;tan,cos,sin0000xyxy则,00POMOMP∽,,00同号与同号与xxyy;sin,00ryyryy;cos,00rxxrxx.tan,00xyxyxy22yxr求三角函数值的两种方法.tan,cos,sinxyrxryP(x,y)为α的终边与单位圆的交点，则r=1..tan,cos,sinxyxy则.135)12(:22OPr析.125tan,1312cos,135sin...