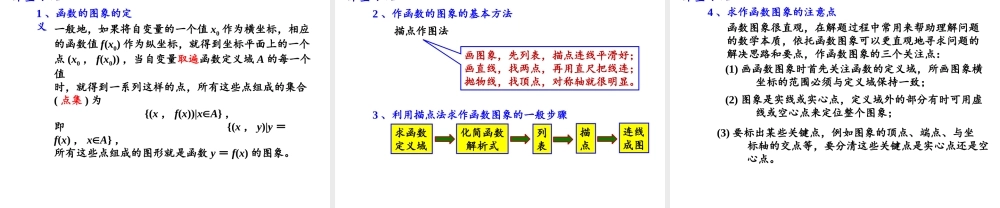
1、函数的图象的定义一般地,如果将自变量的一个值x0作为横坐标,相应的函数值f(x0)作为纵坐标,就得到坐标平面上的一个点(x0,f(x0)),当自变量取遍函数定义域A的每一个值时,就得到一系列这样的点,所有这些点组成的集合(点集)为{(x,f(x))|xA},即{(x,y)|y=f(x),xA},所有这些点组成的图形就是函数y=f(x)的图象。复习回顾画图象,先列表,描点连线平滑好;画直线,找两点,再用直尺把线连;抛物线,找顶点,对称轴就很明显。2、作函数的图象的基本方法描点作图法3、利用描点法求作函数图象的一般步骤列表描点连线成图求函数定义域化简函数解析式复习回顾4、分段函数的概念在定义域内不同的部分上,有不同的解析表达式的函数通常叫做分段函数。(1)分段函数是一个函数,而不是几个函数;(2)分段函数的定义域是几部分的并集;(3)定义域的不同部分不能有相交部分。复习回顾问题诊断1、如果二次函数的图象开口向上且关于直线x=1对称,且过点(0,0),则此二次函数的解析式可以是()(A)f(x)=x2-1(B)f(x)=-(x-1)2+1(C)f(x)=(x-1)2+1(D)f(x)=(x-1)2-12、函数y=-ax+1与y=ax2在同一坐标系中的图象大致是图中的________数学应用例1、人口数量变化趋势是我们制定一系列相关政策的依据,从中国的统计年鉴中可以查得我国1979~2014年人口数据资料(年末)如下表所示,如果把人口数y(百万)看成年份x的函数,试根据下表画出这个函数的图象。年份19791984198919941999200420092014人口数/百万9751044112711991258130013351368类型一求作实际应用问题函数的图象数学建构函数图象很直观,在解题过程中常用来帮助理解问题的数学本质,依托函数图象可以更直观地寻求问题的解决思路和要点,作函数图象的三个关注点:求作函数图象的注意点(1)画函数图象时首先关注函数的定义域,所画图象横坐标的范围必须与定义域保持一致;(2)图象是实线或实心点,定义域外的部分有时可用虚线或空心点来定位整个图象;(3)要标出某些关键点,例如图象的顶点、端点、与坐标轴的交点等,要分清这些关键点是实心点还是空心点。变式拓展某同学从家里到学校,为了不迟到,先跑,跑累了再走余下的路,设在途中花的时间为t,离开家里的路程为d,下面图形中,能反映该同学的行程的是()数学应用类型二函数图象的应用思考:①若x1