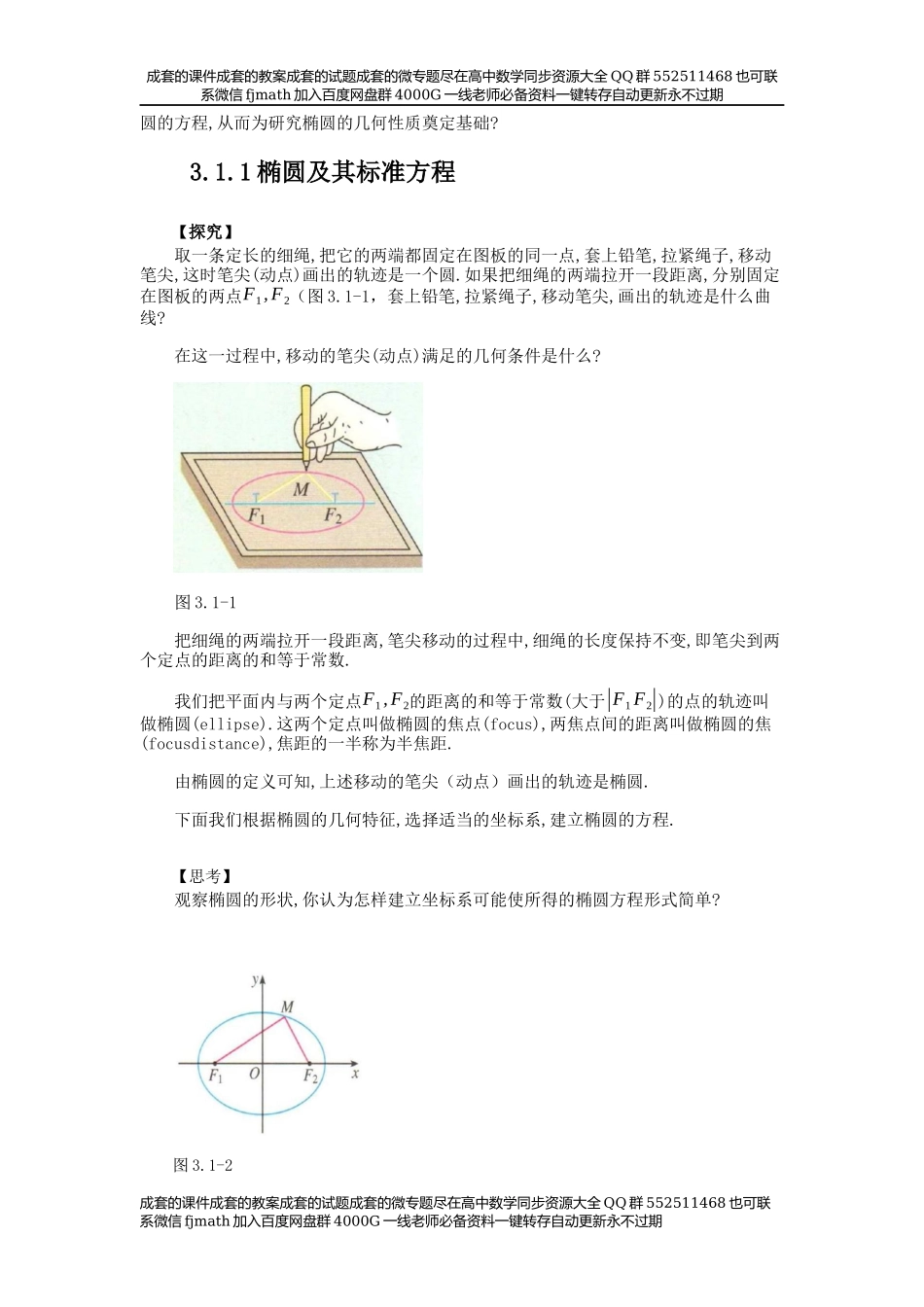
成套的课件成套的教案成套的试题成套的微专题尽在高中数学同步资源大全QQ群552511468也可联系微信fjmath加入百度网盘群4000G一线老师必备资料一键转存自动更新永不过期成套的课件成套的教案成套的试题成套的微专题尽在高中数学同步资源大全QQ群552511468也可联系微信fjmath加入百度网盘群4000G一线老师必备资料一键转存自动更新永不过期第3章圆锥曲线的方程【章头语】我们知道,用一个垂直于圆锥的轴的平面截圆锥,截口曲线(截面与圆锥侧面的交线)是一个圆.如果改变圆锥的轴与截平面所成的角,那么会得到怎样的曲线呢?如图,用一个不垂直于圆锥的轴的平面截圆锥,当圆锥的轴与截面所成的角不同时,可以得到不同的截口曲线,它们分别是椭圆、抛物线和双曲线.我们通常把椭圆、抛物线、双曲线统称为圆锥曲线(conicsections).圆锥曲线与科研、生产以及人类生活有着紧密的关系.如行星绕太阳运行的轨道是椭圆,发电厂冷却塔的外形线是双曲线,探照灯反射镜面、卫星接收天线是抛物线绕其对称轴旋转所成的抛物面⋯⋯为什么圆雉曲线有如此广泛的应用呢?我们可以从它们的几何特征及其性质中找到答案.圆锥曲线的发现与研究始于古希腊.当时人们用纯几何的方法研究这些与圆密切相关的曲线,它们的几何性质是圆的几何性质的自然推广.17世纪,笛卡儿发明了坐标系,人们开始借助坐标系,运用代数方法研究圆锥曲线.本章我们继续采用坐标法,在探究圆锥曲线几何特征的基础上,建立它们的方程,通过方程研究它们的性质,并解决与圆锥曲线有关的几何问题和实际问题,进一步感受数形结合的思想方法,体会坐标法的魅力与威力.3.1椭圆【节引言】椭圆是圆雉曲线的一种,具有丰富的几何性质在科研、生产和人类生活中具有广泛的应用.那么,椭圆到底有怎样的几何特征?我们该如何利用这些特征建立椭成套的课件成套的教案成套的试题成套的微专题尽在高中数学同步资源大全QQ群552511468也可联系微信fjmath加入百度网盘群4000G一线老师必备资料一键转存自动更新永不过期成套的课件成套的教案成套的试题成套的微专题尽在高中数学同步资源大全QQ群552511468也可联系微信fjmath加入百度网盘群4000G一线老师必备资料一键转存自动更新永不过期圆的方程,从而为研究椭圆的几何性质奠定基础?3.1.1椭圆及其标准方程【探究】取一条定长的细绳,把它的两端都固定在图板的同一点,套上铅笔,拉紧绳子,移动笔尖,这时笔尖(动点)画出的轨迹是一个圆.如果把细绳的两端拉开一段距离,分别固定在图板的两点F1,F2(图3.1-1,套上...