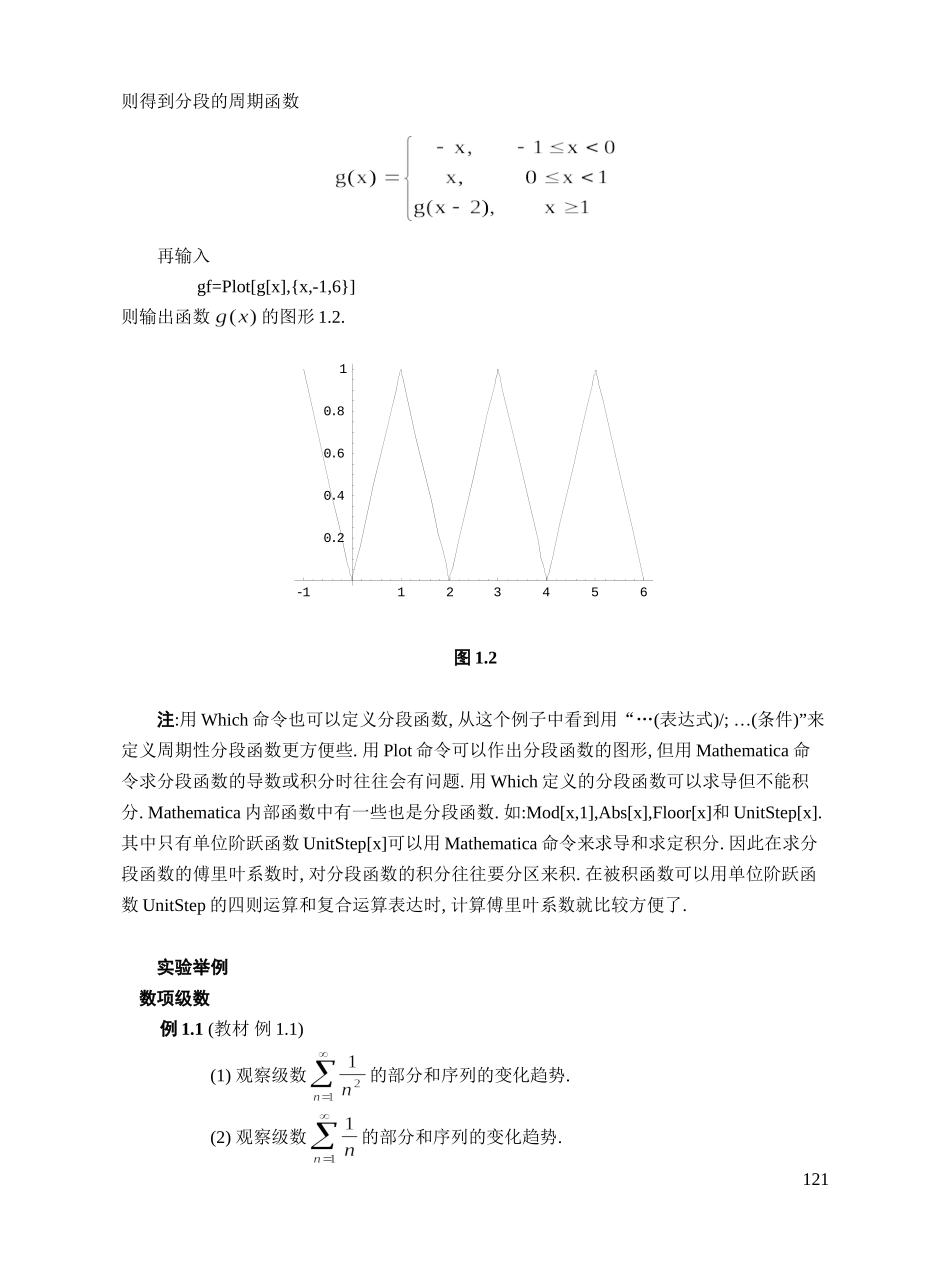
项目四无穷级数与微分方程实验1无穷级数(基础实验)实验目的观察无穷级数部分和的变化趋势,进一步理解级数的审敛法以及幂级数部分和对函数的逼近.掌握用Mathematica求无穷级数的和,求幂级数的收敛域,展开函数为幂级数以及展开周期函数为傅里叶级数的方法.基本命令1.求无穷和的命令Sum该命令可用来求无穷和.例如,输入Sum[1/n^2,{n,l,Infinity}]则输出无穷级数的和为命令Sum与数学中的求和号相当.2.将函数展开为幂级数的命令Series该命令的基本格式为Series[f[x],{x,x0,n}]它将展开成关于的幂级数.幂级数的最高次幂为余项用表示.例如,输入Series[y[x],{x,0,5}]则输出带皮亚诺余项的麦克劳林级数3.去掉余项的命令Normal在将展开成幂级数后,有时为了近似计算或作图,需要把余项去掉.只要使用Normal命令.例如,输入Series[Exp[x],{x,0,6}]Normal[%]则输出1194.强制求值的命令Evaluate如果函数是用Normal命令定义的,则当对它进行作图或数值计算时,可能会出现问题.例如,输入fx=Normal[Series[Exp[x],{x,0,3}]]Plot[fx,{x,-3,3}]则只能输出去掉余项后的展开式而得不到函数的图形.这时要使用强制求值命令Evaluate,改成输入Plot[Evaluate[fx],{x,-3,3}]则输出上述函数的图形.5.作散点图的命令ListPlotListPlot[]为平面内作散点图的命令,其对象是数集,例如,输入ListPlot[Table[j^2,{j,16}],PlotStyle->PointSize[0,012]]则输出坐标为的散点图(图1.1).2.557.51012.51550100150200250图1.16.符号“/;”用于定义某种规则,“/;”后面是条件.例如,输入Clear[g,gf];g[x_]:=x/;0<=x<1g[x_]:=-x/;-1<=x<0g[x_]:=g[x–2]/;x>=1120则得到分段的周期函数再输入gf=Plot[g[x],{x,-1,6}]则输出函数的图形1.2.-11234560.20.40.60.81图1.2注:用Which命令也可以定义分段函数,从这个例子中看到用“…(表达式)/;…(条件)”来定义周期性分段函数更方便些.用Plot命令可以作出分段函数的图形,但用Mathematica命令求分段函数的导数或积分时往往会有问题.用Which定义的分段函数可以求导但不能积分.Mathematica内部函数中有一些也是分段函数.如:Mod[x,1],Abs[x],Floor[x]和UnitStep[x].其中只有单位阶跃函数UnitStep[x]可以用Mathematica命令来求导和求定积分.因此在求分段函数的傅里叶系数时,对分段函数的积分往往要分区来积.在被积函数可以用单位阶跃函数UnitStep的四则运算和复合运算表达时,计算傅里叶系数就比较方便了.实验举例数项级数例1.1(教材例1.1)(1)观察级数的部分和序列的...