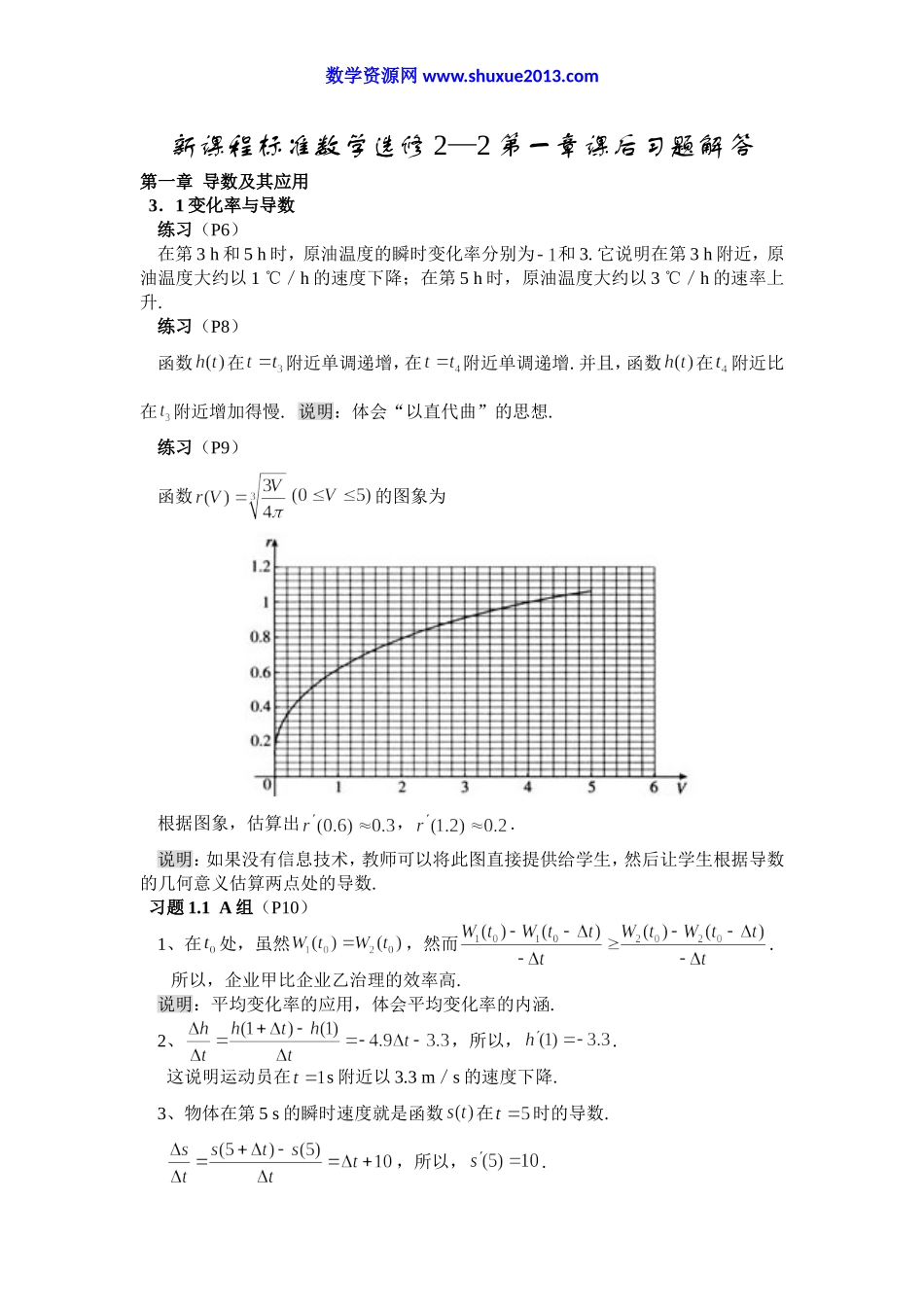
数学资源网www.shuxue2013.com新课程标准数学选修2—2第一章课后习题解答第一章导数及其应用3.1变化率与导数练习(P6)在第3h和5h时,原油温度的瞬时变化率分别为和3.它说明在第3h附近,原油温度大约以1℃/h的速度下降;在第5h时,原油温度大约以3℃/h的速率上升.练习(P8)函数在附近单调递增,在附近单调递增.并且,函数在附近比在附近增加得慢.说明:体会“以直代曲”的思想.练习(P9)函数的图象为根据图象,估算出,.说明:如果没有信息技术,教师可以将此图直接提供给学生,然后让学生根据导数的几何意义估算两点处的导数.习题1.1A组(P10)1、在处,虽然,然而.所以,企业甲比企业乙治理的效率高.说明:平均变化率的应用,体会平均变化率的内涵.2、,所以,.这说明运动员在s附近以3.3m/s的速度下降.3、物体在第5s的瞬时速度就是函数在时的导数.,所以,.数学资源网www.shuxue2013.com因此,物体在第5s时的瞬时速度为10m/s,它在第5s的动能J.4、设车轮转动的角度为,时间为,则.由题意可知,当时,.所以,于是.车轮转动开始后第3.2s时的瞬时角速度就是函数在时的导数.,所以.因此,车轮在开始转动后第3.2s时的瞬时角速度为.说明:第2,3,4题是对了解导数定义及熟悉其符号表示的巩固.5、由图可知,函数在处切线的斜率大于零,所以函数在附近单调递增.同理可得,函数在,,0,2附近分别单调递增,几乎没有变化,单调递减,单调递减.说明:“以直代曲”思想的应用.6、第一个函数的图象是一条直线,其斜率是一个小于零的常数,因此,其导数的图象如图(1)所示;第二个函数的导数恒大于零,并且随着的增加,的值也在增加;对于第三个函数,当小于零时,小于零,当大于零时,大于零,并且随着的增加,的值也在增加.以下给出了满足上述条件的导函数图象中的一种.说明:本题意在让学生将导数与曲线的切线斜率相联系.习题3.1B组(P11)1、高度关于时间的导数刻画的是运动变化的快慢,即速度;速度关于时间的导数刻画的是速度变化的快慢,根据物理知识,这个量就是加速度.2、数学资源网www.shuxue2013.com说明:由给出的的信息获得的相关信息,并据此画出的图象的大致形状.这个过程基于对导数内涵的了解,以及数与形之间的相互转换.3、由(1)的题意可知,函数的图象在点处的切线斜率为,所以此点附近曲线呈下降趋势.首先画出切线的图象,然后再画出此点附近函数的图象.同理可得(2)(3)某点处函数图象的大致形状.下面是一种参考答案.说明:这是...