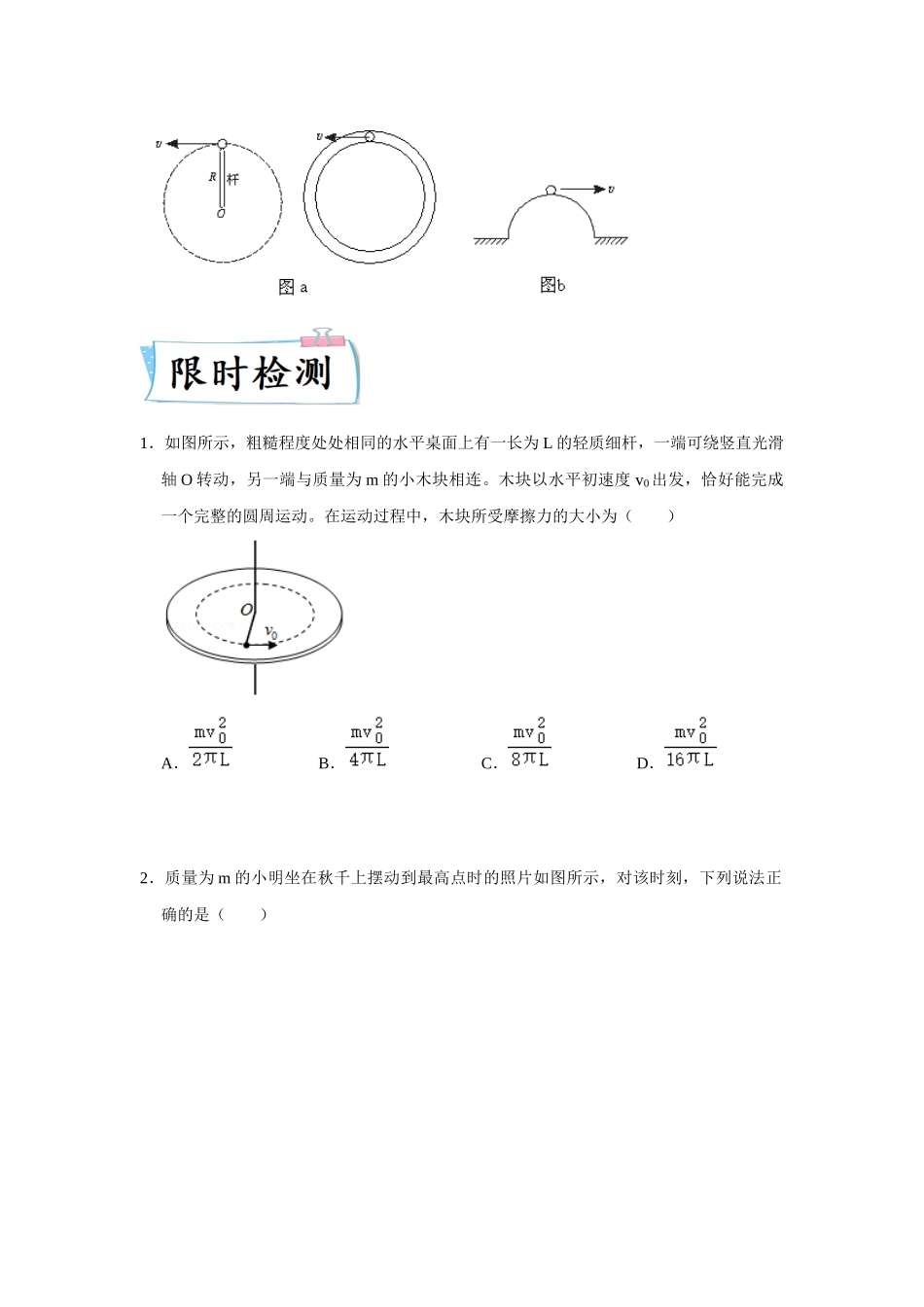
热点05圆周运动圆周运动作为新高考必考的内容之一,对考生的掌握水平相对较高,主要有以下几个方面。第一,掌握圆周运动中线速度,角速度,周期,半径之间的内在联系,能够处理相关问题,主要指生活中常见的联动问题。第二,理解向心力的由来,会分析和计算向心力明白杆,轨道,绳子模型之间的内在联系和区别,主要出题在选择题方面。第三,能够和动能定理联系起来,处理较为复杂的生活实际问题,主要出题在计算题,难度相对较大。因此,即将作为考生的我们,必须对圆周运动有一定的了解,能独立的推导向心力的,并且具备解决相关问题的策略和能力。下面,让我们一起看看下面的这些真题,看看大家的掌握水平,并且好好应用相关的技巧。(1)确定向心力的来源。向心力是根据力的效果命名的,在分析做圆周运动的质点受力情况时,切不可在物体的相互作用力(重力、弹力、摩擦力等)以外再添加一个向心力。(2)确定研究对象的轨道平面和圆心的位置,以便确定向心力的方向。例如,沿半球形碗的光滑内表面,一小球在水平面上做匀速圆周运动,如图所示,小球做圆周运动的圆心在与小球同一水平面上的O′点,而不是在球心O,也不在弹力FN所指的PO线上。(3)物体在静摩擦力作用下做匀速圆周运动时,相对滑动的临界条件是恰好达到最大静摩擦力。(4)物体在不同支承物(绳、杆、轨道、管道等)作用下,在竖直平面做圆周运动,通过最高点时的临界条件。①轻绳模型如图所示没有物体支撑的小球,在竖直平面做圆周运动过最高点的情况:注意:绳对小球只能产生沿绳收缩方向的拉力临界条件:绳子或轨道对小球没有力的作用:得(可理解为恰好转过或恰好转不过的速度)能过最高点的条件:,当时,绳对球产生拉力,轨道对球产生压力.不能过最高点的条件:,实际上球还没到最高点时就脱离了轨道.②轻杆模型(2)如图(a)的球过最高点时,轻质杆(管)对球产生的弹力情况:注意:杆与绳不同,杆对球既能产生拉力,也能对球产生支持力,管壁支撑情况与杆一样。当v=0时,N=mg(N为支持力)当时,N随v增大而减小,且,N为支持力.当v=√Rg时,N=0当v>√Rg时,N为拉力,N随v的增大而增大若是图(b)的小球,此时将脱离轨道做平抛运动,因为轨道对小球不能产生拉力.1.如图所示,粗糙程度处处相同的水平桌面上有一长为L的轻质细杆,一端可绕竖直光滑轴O转动,另一端与质量为m的小木块相连。木块以水平初速度v0出发,恰好能完成一个完整的圆周运动。在运动过程中,木块...