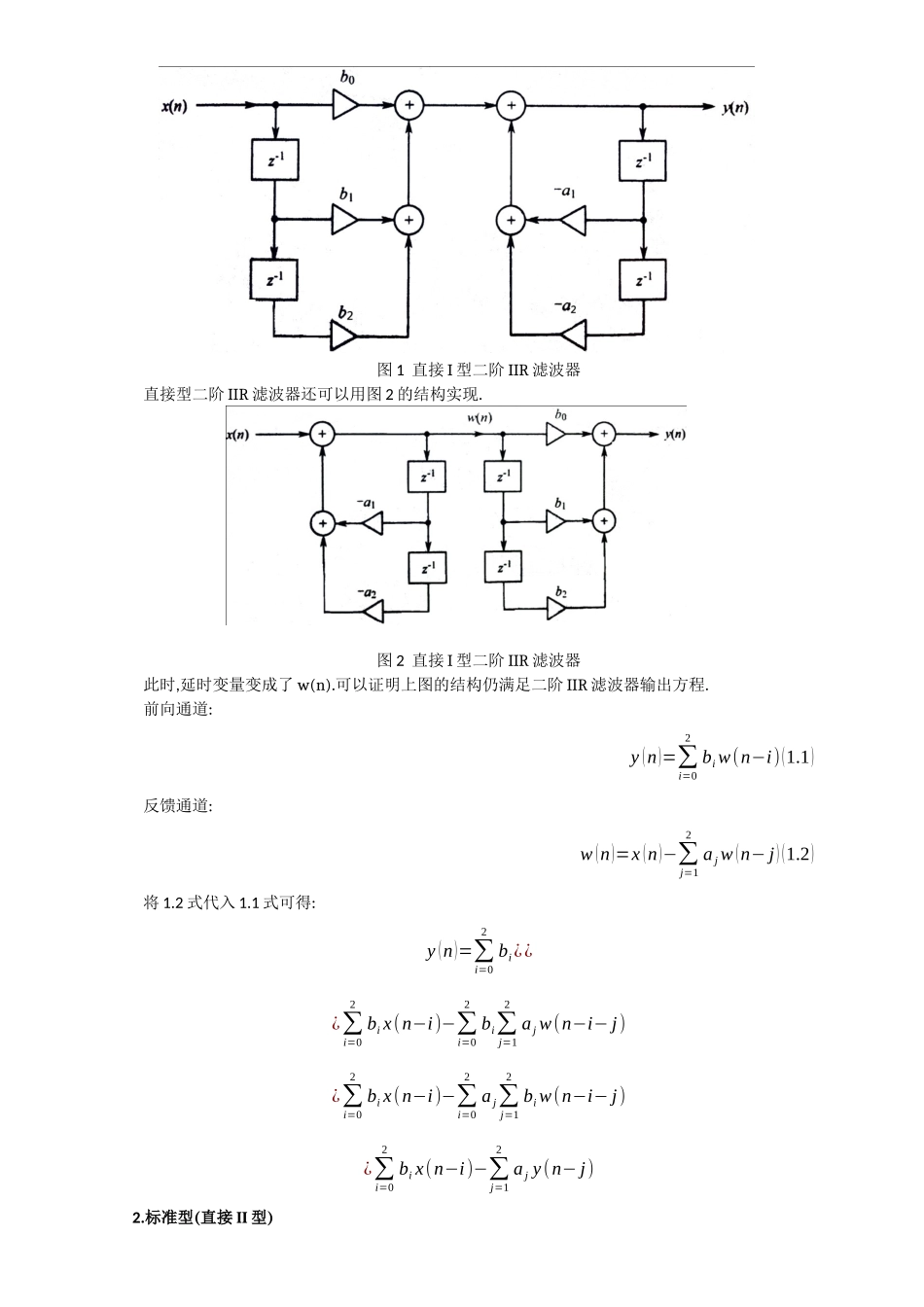
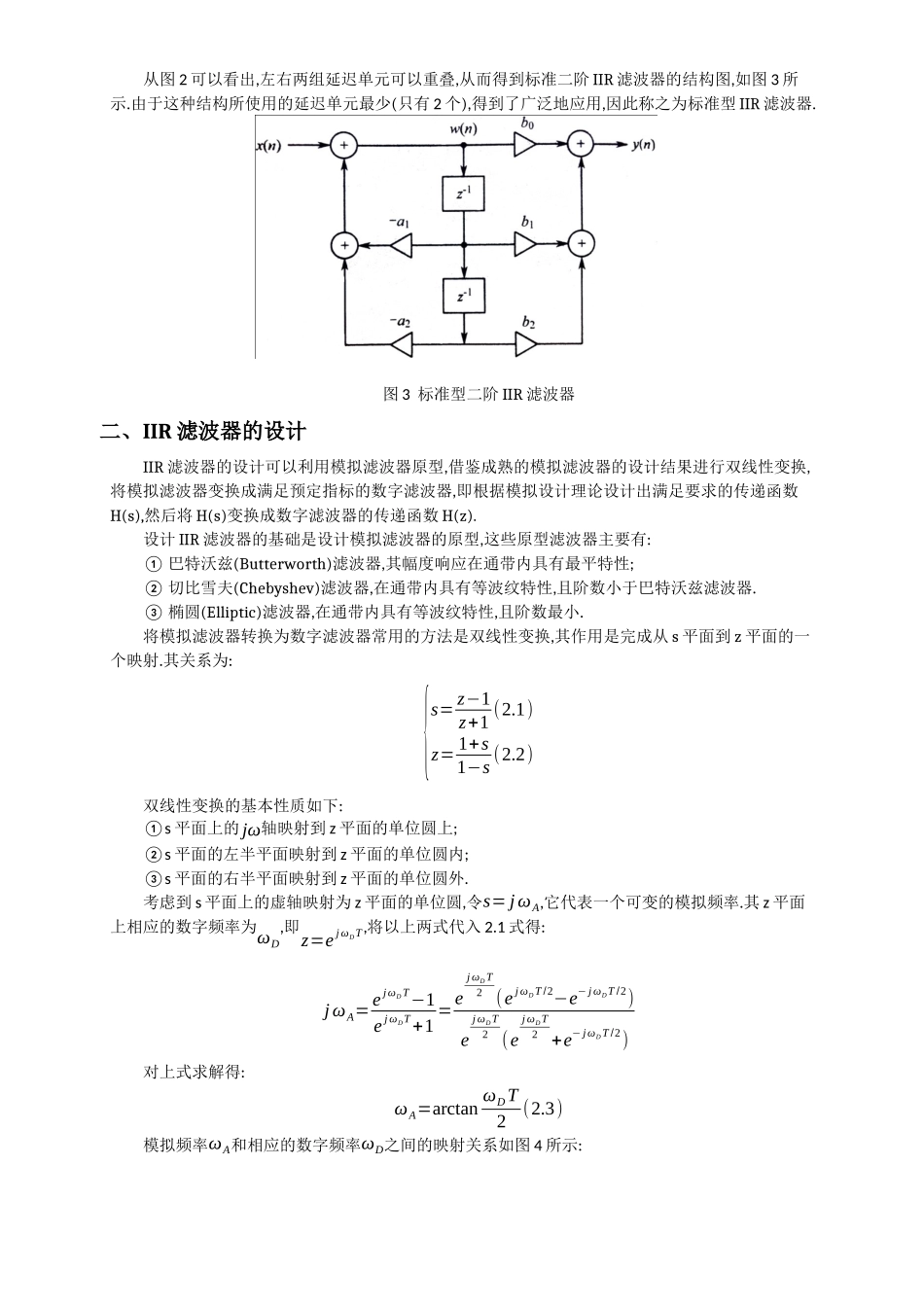
IIR滤波器的DSP实现一、IIR滤波器的基本结构IIR滤波器差分方程的一般表达式为:y(n)=∑i=0Nbix(n−i)−∑i=1Maiy(n−i)式中x(n)为输入序列;y(n)为输出序列;ai和bi为滤波器系数.若所有系数ai等于0,则为FIR滤波器.IIR滤波器具有无限长的单位脉冲响应,在结构上存在反馈回路,具有递归性,即IIR滤波器的输出不仅与输入有关,而且与过去的输出有关.将上式展开得出y(n)表达式为:y(n)=b0x(n)+b1x(n−1)+…+bNx(n−N)−a1y(n−1)−a2y(n−2)−…−aMy(n−M)在零初始条件下,对上式进行z变换,得到:Y(z)=b0X(z)+b1z−1X(z)+…+bNz−NX(z)−a1z−1Y(z)−a2z−2Y(z)−…−aMz−MY(z)设N=M,则传递函数为:H(z)=Y(z)X(z)=b0+b1z−1+…+bNz−N1+a1z−1+…+aNz−N上式可写成:H(z)=b0zN+b1zN−1+…+bNzN+a1z−1+…+aN=C∏i=1Nz−ziz−pi上式具有N个零点zi和N个极点pi.若有极点位于单位圆外将导致系统不稳定.由于FIR滤波器所有的系数ai均为0,不存在极点,不会造成系数的不稳定.对于IIR滤波器,系统稳定的条件如下:若|pi|<1,当n→∞时,h(n)→0,系统稳定;若|pi|>1,当n→∞时,h(n)→∞,系统不稳定.IIR滤波器具有多种形式,主要有:直接型(也称直接I型)、标准型(也称直接II型)、变换型、级联型和并联型.二阶IIR滤波器,又称为二阶基本节,分为直接型、标准型和变换型.对于一个二阶IIR滤波器,其输出可以写成:y(n)=b0x(n)+b1x(n−1)+b2x(n−2)−a1y(n−1)−a2y(n−2)1.直接型(直接I型)根据上式可以得到直接二型IIR滤波器的结构图.如图1所示.共使用了4个延迟单元(z−1).图1直接I型二阶IIR滤波器直接型二阶IIR滤波器还可以用图2的结构实现.图2直接I型二阶IIR滤波器此时,延时变量变成了w(n).可以证明上图的结构仍满足二阶IIR滤波器输出方程.前向通道:y(n)=∑i=02biw(n−i)(1.1)反馈通道:w(n)=x(n)−∑j=12ajw(n−j)(1.2)将1.2式代入1.1式可得:y(n)=∑i=02bi¿¿¿∑i=02bix(n−i)−∑i=02bi∑j=12ajw(n−i−j)¿∑i=02bix(n−i)−∑i=02aj∑j=12biw(n−i−j)¿∑i=02bix(n−i)−∑j=12ajy(n−j)2.标准型(直接II型)从图2可以看出,左右两组延迟单元可以重叠,从而得到标准二阶IIR滤波器的结构图,如图3所示.由于这种结构所使用的延迟单元最少(只有2个),得到了广泛地应用,因此称之为标准型IIR滤波器.图3标准型二阶IIR滤波器二、IIR滤波器的设计IIR滤波器的设计可以利用模拟滤波器原型,借鉴成熟的模拟滤波器的设计结果进行双线性变换,将模拟滤波器变换成满足预定指标的数字滤波器,即根据模拟设计...