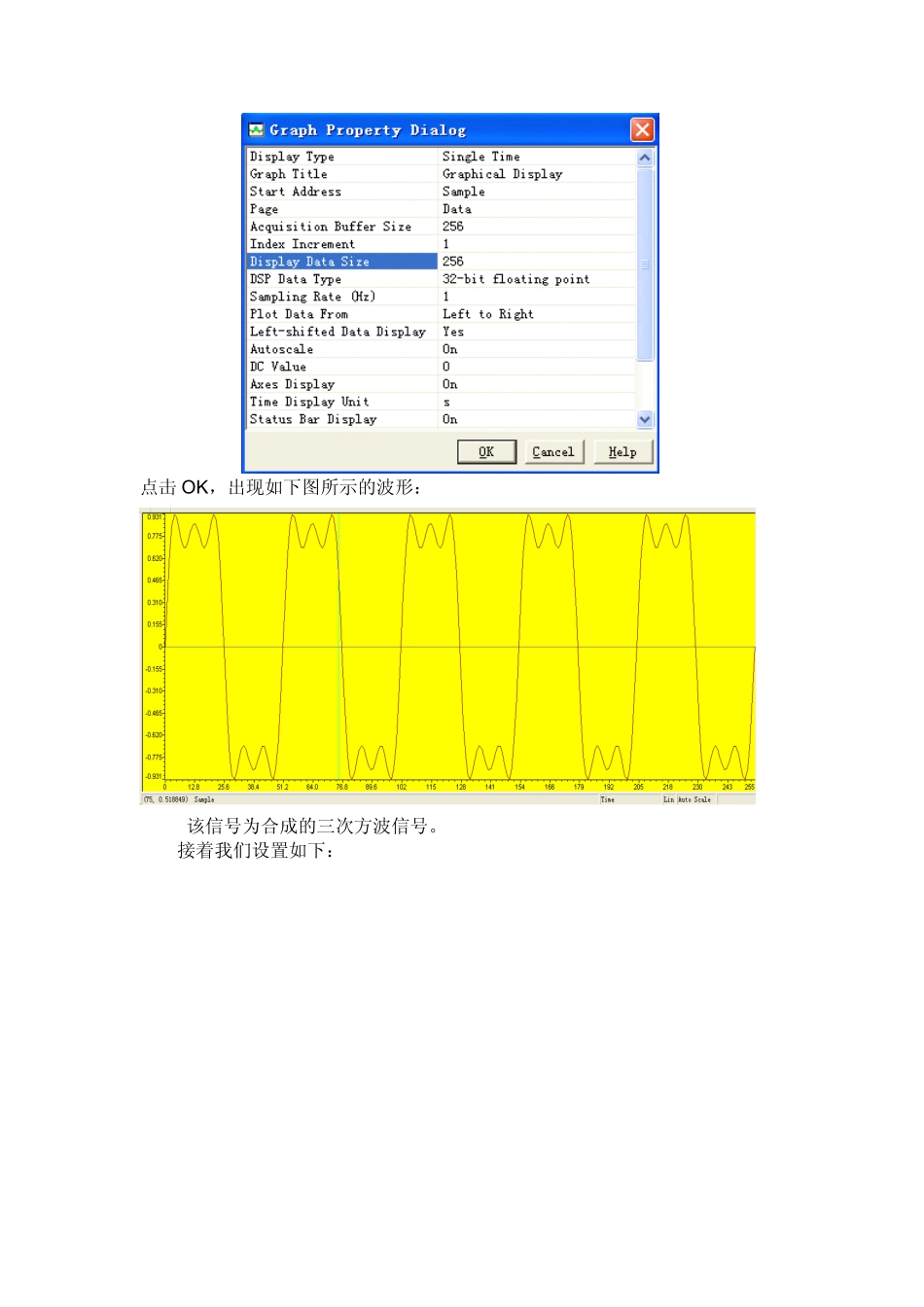
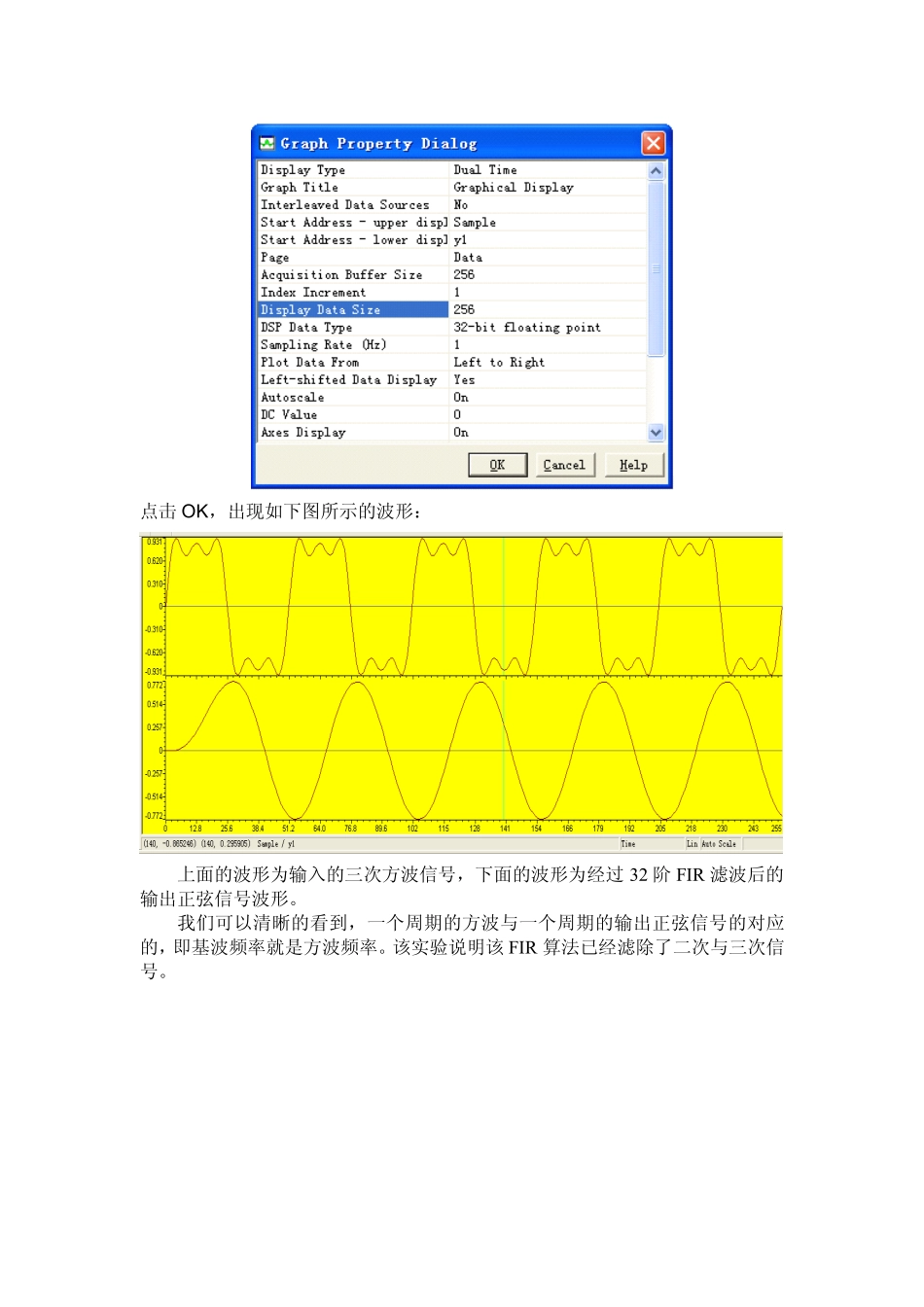
FIR(FiniteImpulseResponse)滤波器:有限长单位冲激响应滤波器,是数字信号处理系统中最基本的元件,它可以在保证任意幅频特性的同时具有严格的线性相频特性,同时其单位抽样响应是有限长的,因而滤波器是稳定的系统。因此,FIR滤波器在通信、图像处理、模式识别等领域都有着广泛的应用。算法原理:离散信号序列通过一个离散滤波系统,得到离散输出信号,如果滤波系统的单位脉冲响应为h(n),信号序列为x(n),输出信号为y(n),则使用运算关系式表达他们之间的关系如下:∑∞−∞=−=∗=mmnhmxnhnxny)()()()()(输入信号与系统响应之间的运算关系为线性卷积。根据这样的关系,我们至少有两种方法实现FIR:1、直接卷积法:根据卷积的迭代运算直接计算输入信号序列与滤波系数的卷积,得到滤波输出信号,此法运算关系简单,但耗时较长;2、快速卷积法:有时域与频域的对于关系,使用FFT算法实现FIR,此法与直接卷积法相比,相同的点数下运算时间短,而且点数越多相对时间就越短,但是算法关系复杂。本实验使用第一种方法,调用卷积函数实现对一段信号的滤波(卷积函数的算法原理参见用户手册《卷积算法实验说明》)。验证方法:使用一段合成的256点三次方波信号作为采样后的信号序列,设计一个窗函数滤波除掉二次与三次谐波,输出基次谐波应该为一段正弦波。为确定合成信号的输出频率,将该合成信号经过DA输出,在示波器上观察到其频率为420Hz,即其基波频率为420Hz。确定滤波器的截止频率为500Hz,采样频率为128000Hz,滤波器阶数为32阶,采用汉宁窗。使用MATLAB工具中的FDATOOL功能很简便的得到的满足上述要求的滤波器系数。打开FIR滤波器例程FIR加载到开发板中运行,点击view->Graph->Time/Frequency,设置如下:点击OK,出现如下图所示的波形:该信号为合成的三次方波信号。接着我们设置如下:点击OK,出现如下图所示的波形:上面的波形为输入的三次方波信号,下面的波形为经过32阶FIR滤波后的输出正弦信号波形。我们可以清晰的看到,一个周期的方波与一个周期的输出正弦信号的对应的,即基波频率就是方波频率。该实验说明该FIR算法已经滤除了二次与三次信号。