第二章习题答案.pdfVIP免费

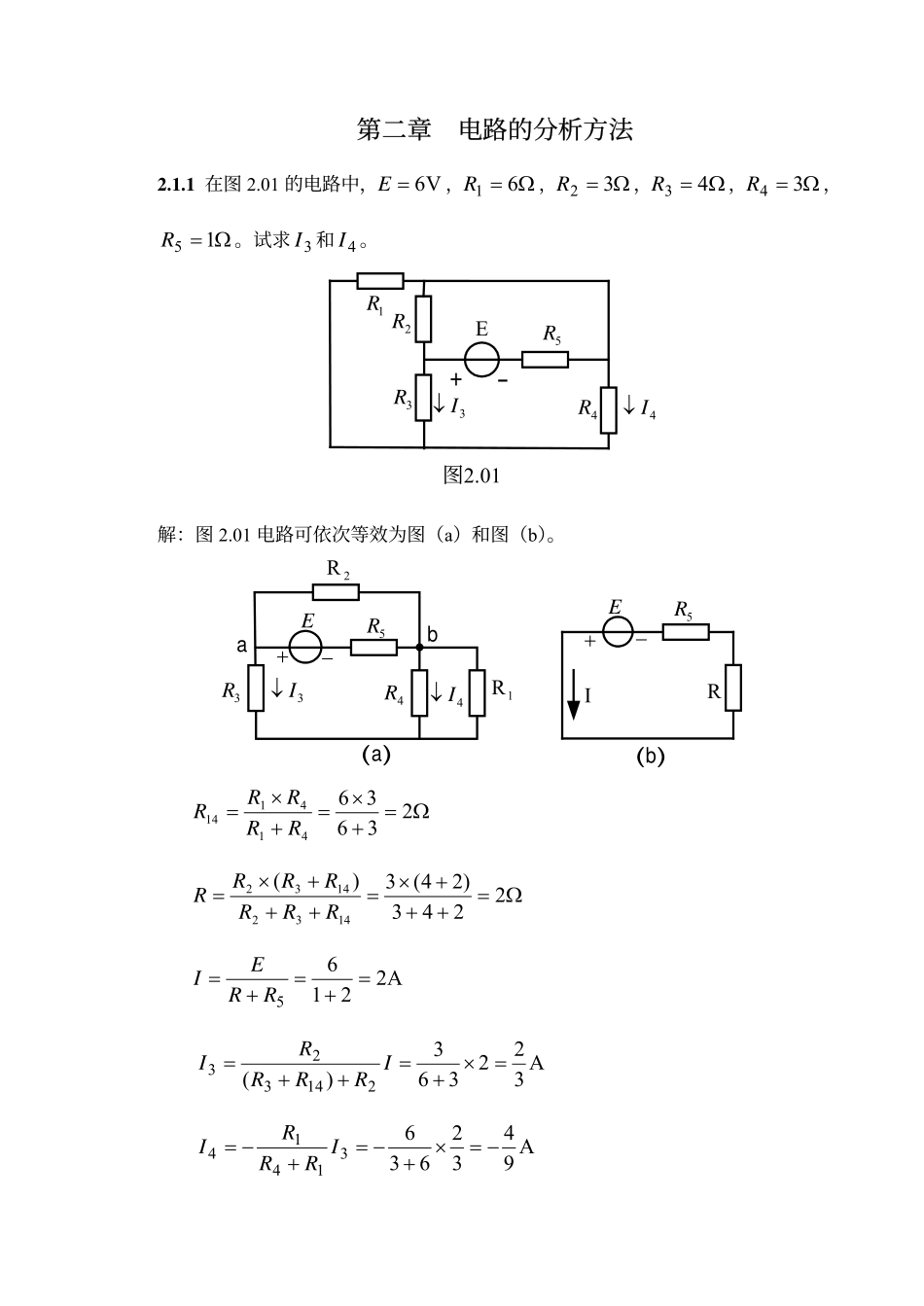
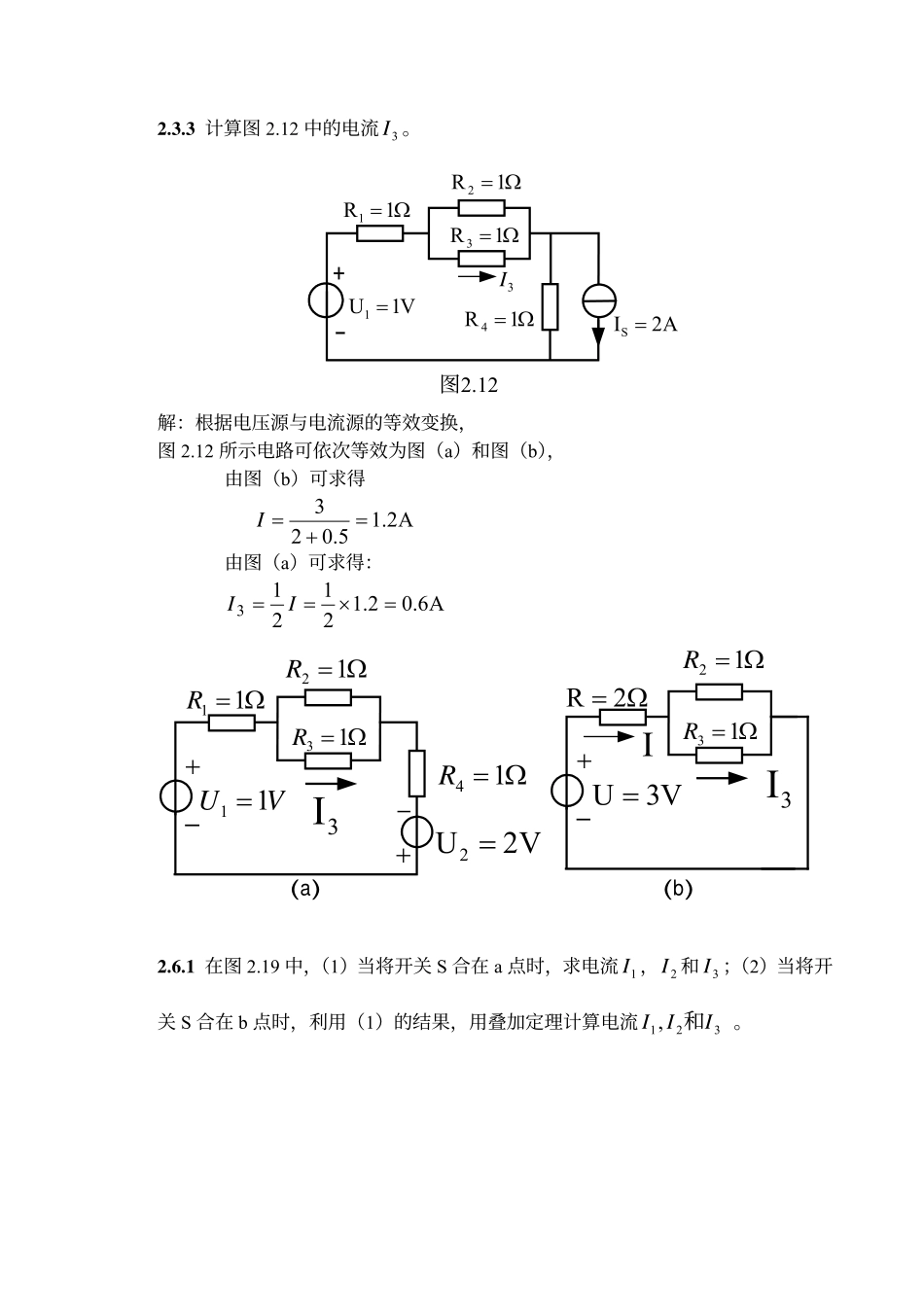
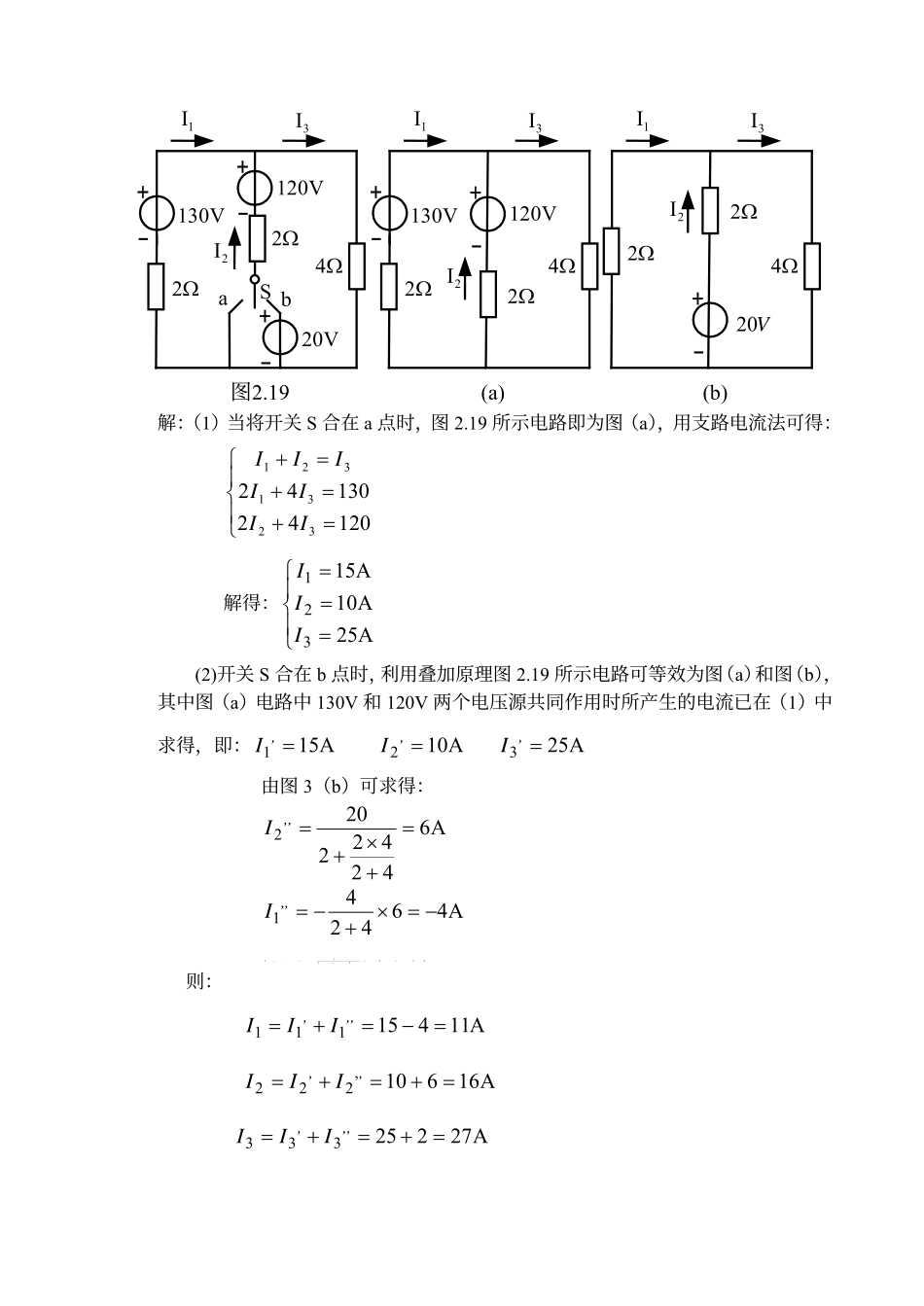
第二章电路的分析方法2.1.1在图2.01的电路中，V6=E，Ω=61R，Ω=32R，Ω=43R，Ω=34R，Ω=15R。试求3I和4I。1R2R3R4R5R4I↓3I↓E+-图2.01解：图2.01电路可依次等效为图（a）和图（b）。2R3R4R5R4I↓3I↓+−Ea1R(a)bI5R+−ER(b)Ω=+×=+×=23636414114RRRRRΩ=+++×=+++×=2243)24(3)(14321432RRRRRRRA22165=+=+=RREIA322363)(214323=×+=++=IRRRRIA943263631414−=×+−=+−=IRRRI2.3.3计算图2.12中的电流3I。V1U1=Ω=1R1Ω=1R2Ω=1R3A2IS=Ω=1R4+-图2.123I解：根据电压源与电流源的等效变换，图2.12所示电路可依次等效为图（a）和图（b），由图（b）可求得A2.15.023=+=I由图（a）可求得：A6.02.121213=×==IIVU11=+−Ω=11RΩ=12RΩ=13RV2U2=Ω=14R−+3I(a)Ω=2RI(b)+−Ω=12RΩ=13R3IV3U=2.6.1在图2.19中，（1）当将开关S合在a点时，求电流1I，2I和3I；（2）当将开关S合在b点时，利用（1）的结果，用叠加定理计算电流321,III和。Ω4abSV20Ω2V120V130Ω23I1I2I+-+-+-图2.19Ω4Ω2V120V130Ω23I1I2I+-+-(a)Ω4Ω2V20Ω23I1I2I+-(b)解：（1）当将开关S合在a点时，图2.19所示电路即为图（a），用支路电流法可得：=+=+=+12042130423231321IIIIIII解得：===A25A10A15321III(2)开关S合在b点时，利用叠加原理图2.19所示电路可等效为图（a）和图（b），其中图（a）电路中130V和120V两个电压源共同作用时所产生的电流已在（1）中求得，即：A151=,IA102=,IA253=,I由图3（b）可求得：A642422202=+×+=,,IA464241−=×+−=,,IA26422,,3=×+=I则：A11415111=−=+=,,,IIIA16610,222=+=+=,,IIIA27225333=+=+=,,,III2.6.2电路如图2.20（a）所示，V10ab,,V124321=====URRRRE。若将理想电压源除去后[图2.20(b)]。试问这时abU等于多少？1R2R3R4RIab+−EI图2.20（a）1R2R3R4RIabI图2.20（b）解：当电压源单独作用时，图2.20所示电路如图4所示，1R3R4Ra+−Eb2R图4这时：V3124141ab=×==EU,根据叠加原理，电流源单独作用时：V7310ababab=−=−=,,,UUU2.7.4在图2.24中，（1）当开关S断开时，试求电阻5R上的电压5U和电流5I；（2）当开关S闭合后，试用戴维宁定理计算5I。已知Ω=Ω=======10,1,V4,V13,V1554321321RRRRREEE。1E2E3E5U1R2R3R4RS5I5R图2.24+-+-+-+-解：（1）当开关S断开时05=U05=I（2）当开关S闭合时，图2.24所示电路5R左右两侧可得两个有源二端网络，如图（a）所示。1E2E3E1R2R3R4R(a)+-+-+-abc++−−−01U02U5U01R02R5I5R(b)+根据戴维宁...