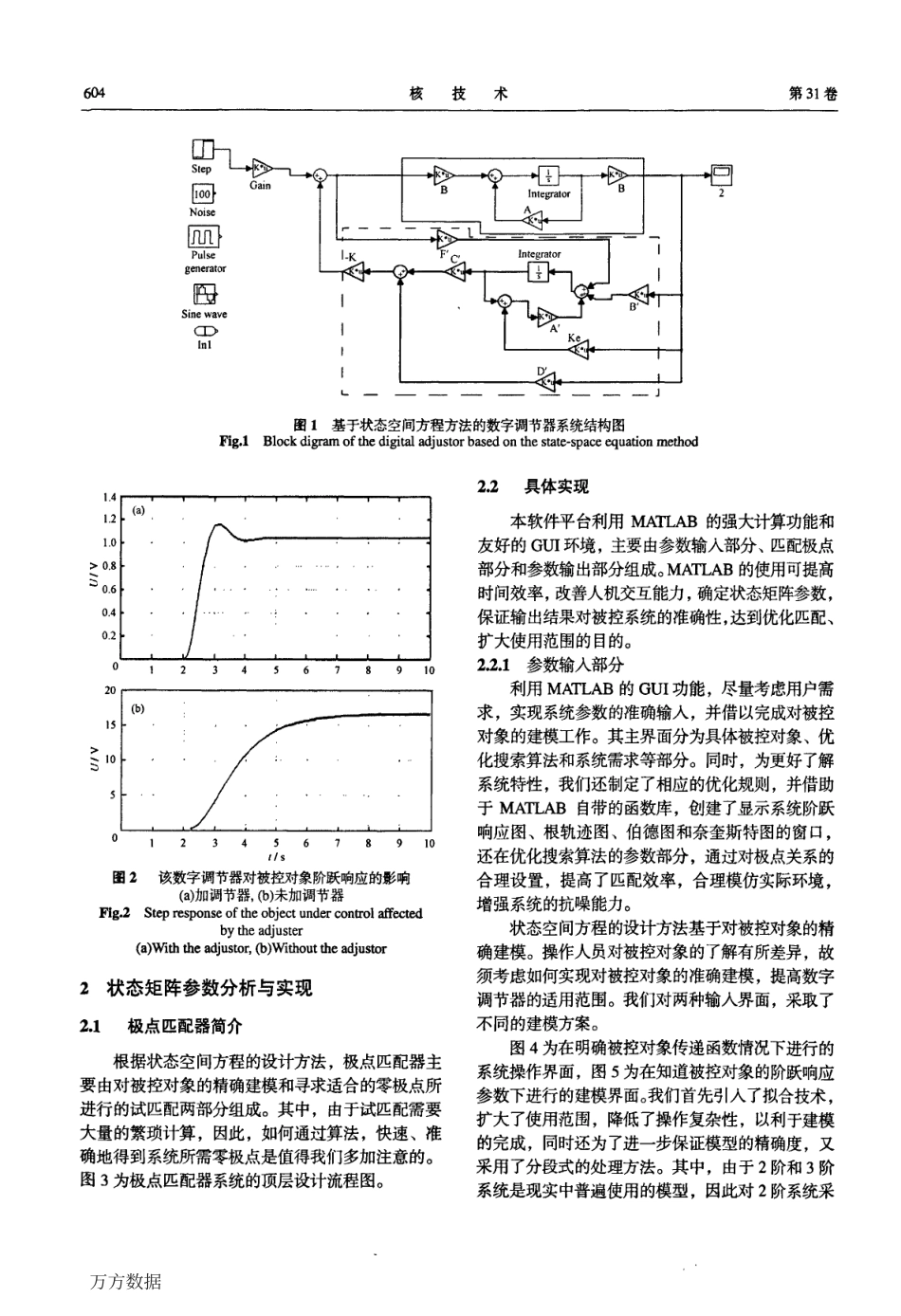
第31卷第8期2008年8月核技术NUCLEARTECHNIQUESV01.31,No.8August2008用于加速器电源的数字调节器的状态矩阵参数分析与实现龙银东1’2乔为民1赵龙1’2敬岚11(中国科学院近代物理研究所兰州730000)2(中国科学院研究生院北京100049)摘要介绍了在基于CyclonelI芯片,采用状态空间方程所实现的数字调节器系统中,必不可少的状态矩阵参数分析与实现的软件平台。通过对算法优化和对MATLAB自带函数的调用,实现了针对被控对象具体需求,精度范围在1064以内的参数获取。同时还加入了极点选取规则,使最终得到的参数更符合实际需求,为实现精确、实时的数字调节器系统提供了必要的保证。关键词极点,MATLAB,数字调节器,状态空间方程中图分类号TP21420世纪80年代,兰州重离子加速器(HIRFL)合成了20多种远离稳定线的新核素,其控制系统也不断更新。随后建设的兰州重离子加速器冷却储存环(HIRFL-CSR),则更须进一步提高系统的稳定性和精确度。随着集成芯片的不断发展和现代控制理论的进一步完善,使用状态空间方程的设计方法,实现高精度、实时的数字调节器,以保证加速器得到更好的束流已成为可能【l】。本文实现的针对状态矩阵参数分析与实现的软件系统,是以CycloneII2C20F484芯片作为硬件平台,以QuartusII5.0作为硬件编程环境,最终开发出的数字调节器系统寻找到适合于具体被控对象和系统响应要求的零极点,从而为加速器电源的改造成功提供重要保证。同时,可根据用户输入的具体被控对象指标,得到适合于不同被控对象的数字调节器参数,为数字调节器普遍使用带来可能,有助于提高此数字调节器的经济效应,降低开发成本,实现整个数字调节器系统的产品化生产口J。1整体设计目前,状态空间方程的设计已成为国际最为先进的控制理论设计方法之一,不仅为系统实现数字化控制带来了可能,还由于它具有针对局部最优化的设计理念,为进一步解决复杂系统的控制问题带来了可行性方法。公式1、2即为状态空间方程设计方法的系统模型表示【3】。X’=AX+Bu(1)Y=CX+Du(2)式中,x为状态向量∽维向量),】,为输出向量(纯量),U为控制信号(纯量)。可选取控制信号:“=.^Ⅸ,其中lxn维矩阵K即为状态反馈增益矩阵。图1为一个单输入单输出的数字调节器系统,实线部分即为具体的被控对象,虚线部分即为针对此被控对象的观测器,左端即为连接的一个阶跃输入信号。实验表明,数字调节器系统不仅能达到万分之一精度和毫秒级的响应要求,还具有状态空间方程设计方法所具有的局...