第六章实际气体方程(1).pdfVIP免费

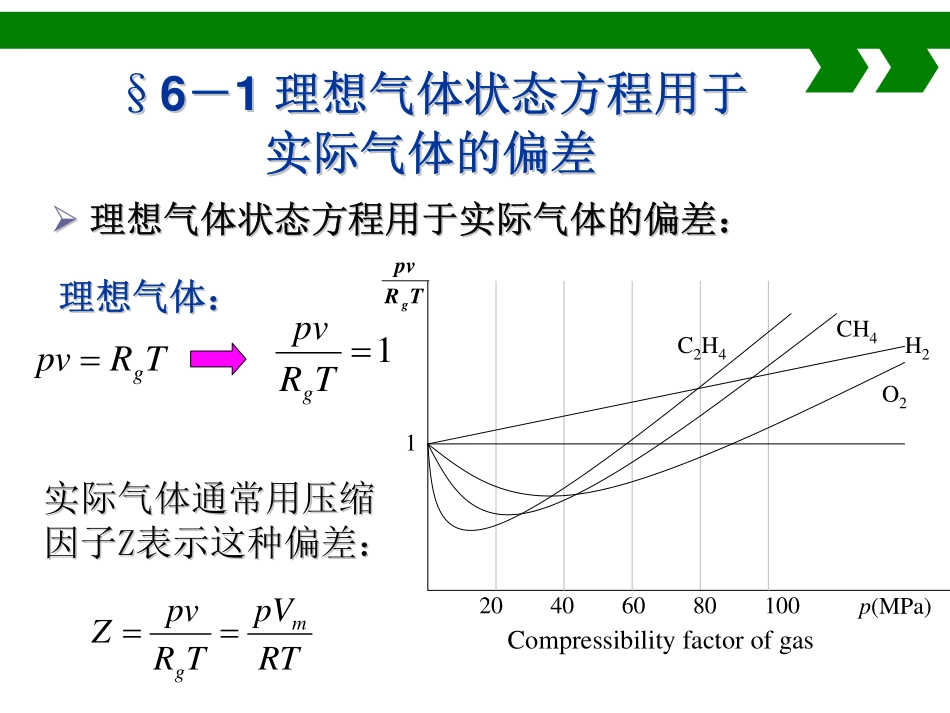
第六章实际气体的性质及热力学一般关系前面章节所推导的热力学关系式都是针对理想气体而言的，实际情况下，如水蒸气、氨气等都不满足理想气体假设。本章讨论的就是热力学的一般关系。1、实际气体状态方程；2、利用压缩因子图求解实际气体状态参数；3、热力学能、焓、熵和比热容的一般关系式；基本要求TRpvg§§66－－11理想气体状态方程用于理想气体状态方程用于实际气体的偏差实际气体的偏差理想气体：理想气体：1TRpvg理想气体状态方程用于实际气体的偏差：理想气体状态方程用于实际气体的偏差：实际气体通常用压缩实际气体通常用压缩因子因子ZZ表示这种偏差：表示这种偏差：RTpVTRpvZmgCH4C2H420406080100p(MPa)H2O21CompressibilityfactorofgasTRpvg理想气体理想气体：：ZZ恒等于恒等于11；；实际气体实际气体：：ZZ可大于可大于11，也可小于，也可小于11，，ZZ值偏离值偏离11的大的大小，反映实际气体偏离理想气体的程度。小，反映实际气体偏离理想气体的程度。ZZ值的大小不仅与值的大小不仅与气体种类气体种类有关，而且同种气有关，而且同种气体的体的ZZ值还随值还随压力压力和和温度温度而变化。而变化。iggvvpTRvTRpvZ/ZRTpVRTpVTRpvZmmg或压缩因子Z：其中其中vvii为相同为相同pp、、TT下实际气下实际气体作为理想气体时的比体积体作为理想气体时的比体积§6－2范德瓦尔方程和R-K方程1.气体分子有一定的体积，所以分子可自由活动的空间为（Vm-b）2.气体分子间的引力作用，气体对容器壁面所施加的压力要比理想气体的小，用内压力()修正压力项。一、范德瓦尔方程2mVaJ.D.VonderWaals，荷兰物理学家。1873年发表论文“论气体和液体的连续性”，提出了范德瓦尔方程。22))((mmmmVabVRTpRTbVVap或范德瓦尔方程：范德瓦尔方程：0)(23abaVVRTbppVmmm随着随着pp、、TT不同，不同，VVmm的解有三种可能：的解有三种可能：将范德瓦尔方程按将范德瓦尔方程按VVmm的降幂排列：的降幂排列：其中其中aa、、bb为范德瓦尔常数，与为范德瓦尔常数，与气体种类气体种类有关。有关。三个不等的实根三个不等的实根三个相等的实根三个相等的实根一个实根两个虚根一个实根两个虚根COCO22等温过程实验等温过程实验1869年英国物理学家Andrews用CO2做的等温过程实验。得出不同温度下p-v关系曲线COCO22等温线等温线温度较高（48.1°C以上）、压力较低时，CO2的等温线近似为双曲线，可视为理想气...