几何补充.pptVIP免费

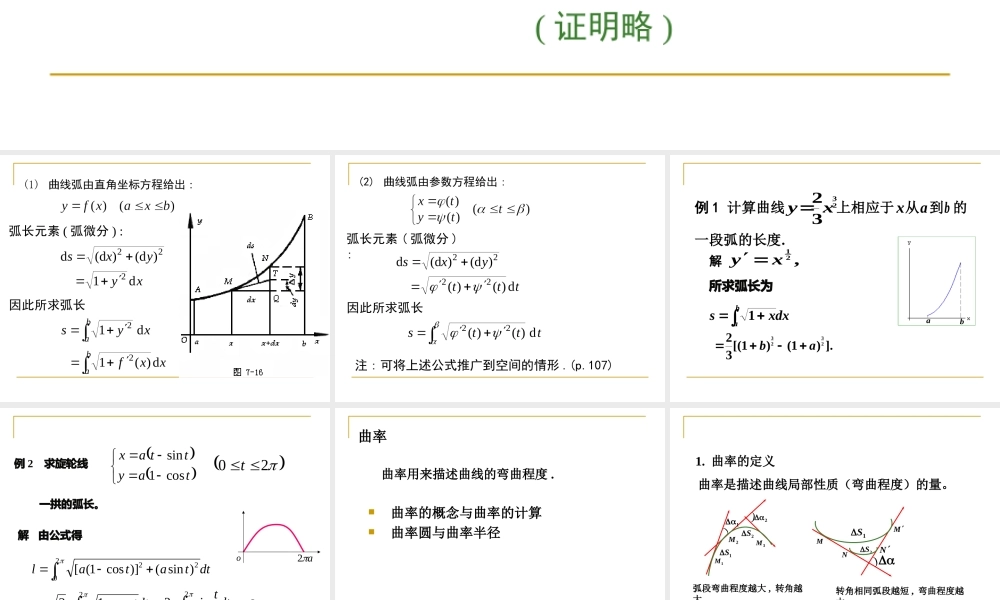
平面曲线的弧长(p.106)定义:若在弧AB上任意作内接折线,0M1iMiMnMAByox当折线段的最大边长→0时,折线的长度趋向于一个确定的极限,此极限为曲线弧AB的弧长,即并称此曲线弧为可求长的.iiMM1定理:任意光滑曲线弧都是可求长的.(证明略)ni10lims则称(1)曲线弧由直角坐标方程给出:弧长元素(弧微分):xyd12因此所求弧长xysbad12xxfbad)(1222)(d)(ddyxs(2)曲线弧由参数方程给出:弧长元素(弧微分):因此所求弧长tttsd)()(22tttd)()(2222)(d)(ddyxs注:可将上述公式推广到空间的情形.(p.107)解12,yx所求弧长为dxxsba1].)1()1[(322323abab例1计算曲线2332xy上相应于x从a到b的一段弧的长度.tayttaxcos1sin例2求旋轮线一拱的弧长。20toa2解由公式得dttatal2022)sin()]cos1([dtta20cos12dtta202sin2.8a曲率曲率用来描述曲线的弯曲程度.曲率的概念与曲率的计算曲率圆与曲率半径曲率是描述曲线局部性质（弯曲程度）的量。1M3M)22M2S1SMM1S2SNN)弧段弯曲程度越大,转角越大转角相同弧段越短,弯曲程度越大1.曲率的定义1)注:曲线的弯曲程度与切线的转角大小成正比,与弧长成反比.)SS).M.MC0Myxo.sKMM的平均曲率为弧段（设曲线C是光滑的，.0是基点M,sMM（.切线转角为MM定义sKs0lim曲线C在点M处的曲率,lim0存在的条件下在dsdss.dsdK例1.求半径为R的圆上任意点处的曲率.解:如图所示,RssKs0limR1可见:R愈小,则K愈大,圆弧弯曲得愈厉害;R愈大,则K愈小,圆弧弯曲得愈小.sRMM注意:直线上任意点处的曲率为0.2.曲率的计算公式,)(二阶可导设xfy,tany,12dxyyd.)1(232yyk,arctany有.12dxyds.dsdK,)()(),(),(二阶可导，设曲线方程为tttytx.)]()([)()()()(2322ttttttk,)()(ttdxdy.)()()()()(322tttttdxyd例2.?2上哪一点的曲率最大抛物线cbxaxy解,2baxy,2ay.])2(1[2232baxak显然,,2时当abx.最大k,)44,2(2为抛物线的顶点又aacbab.最大抛物线在顶点处的曲率例3:...