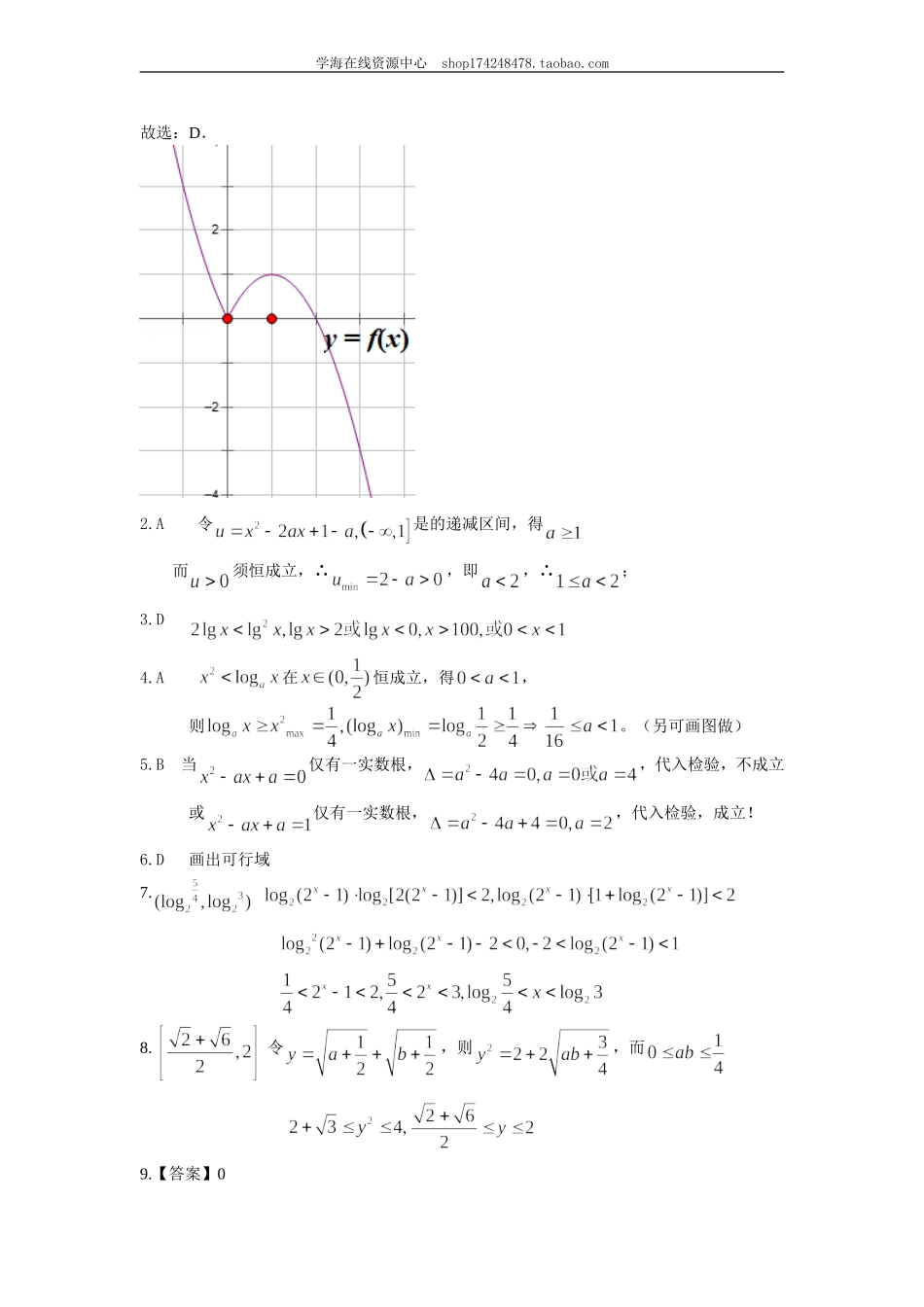
学海在线资源中心shop174248478.taobao.com【巩固练习】1.(2015郑州一模)已知函数f(x)=,若关于x的不等式[f(x)]2+af(x)﹣b2<0恰有1个整数解,则实数a的最大值是()A.2B.3C.5D.82.若在区间上递减,则范围为()A.B.C.D.3.不等式的解集是()A.B.C.D.4.若不等式在内恒成立,则的取值范围是()A.B.C.D.5.若不等式有唯一解,则的取值为()A.B.C.D.6.不等式组的区域面积是()A.B.C.D.7.不等式的解集是_______________。8.已知,则的范围是____________。9.(2016杭州模拟)实数x、y满足,则z=x2+y2+2x2y﹣的最小值为.10.设,则函数在=________时,有最小值__________。学海在线资源中心shop174248478.taobao.com11.不等式的解集是________________。12.若函数的值域为,求实数的取值范围。13.已知△ABC的三边长是,且为正数,求证:。14.解不等式:15.(2015福建模拟)已知不等式|x2|≤1﹣的解集与不等式2x2ax+b﹣<0的解集相同.(Ⅰ)求a,b的值;(Ⅱ)求函数f(x)=a+b的最大值及取得最大值时x的值.16.设函数的值域为,求的值。17.已知实数满足,且有求证:【参考答案与解析】1.【答案】D【解析】函数f(x)=,如图所示,①当b=0时,[f(x)]2+af(x)﹣b2<0化为[f(x)]2+af(x)<0,当a>0时,﹣a<f(x)<0,由于关于x的不等式[f(x)]2+af(x)﹣b2<0恰有1个整数解,因此其整数解为3,又f(3)=9+6=3﹣﹣,∴a﹣<﹣3<0,﹣a≥f(4)=8﹣,则8≥a>3,a≤0不必考虑.②当b≠0时,对于[f(x)]2+af(x)﹣b2<0,△=a2+4b2>0,解得:<f(x)<,只考虑a>0,则<0<,由于f(x)=0时,不等式的解集中含有多与一个整数解(例如,0,2),舍去.综上可得:a的最大值为8.学海在线资源中心shop174248478.taobao.com故选:D.2.A令是的递减区间,得而须恒成立,∴,即,∴;3.D4.A在恒成立,得,则。(另可画图做)5.B当仅有一实数根,,代入检验,不成立或仅有一实数根,,代入检验,成立!6.D画出可行域7.8.令,则,而9.【答案】0学海在线资源中心shop174248478.taobao.com【解析】作出不等式组对应的平面区域,则z=x2+y2+2x2y=z=﹣(x+1)2+(y1﹣)22﹣,设m=(x+1)2+(y1﹣)2,则m的几何意义为区域内的点倒是定点D(﹣1,1)的距离的平方,由图象知D到直线y=x的距离最小,此时d=,则m=d2=2,故z的最小值为z=22=0﹣,故答案为:0.10.11.当时,得;当时,得;12.解:令,则须取遍所有的正实...