LHW第五章.pptVIP免费

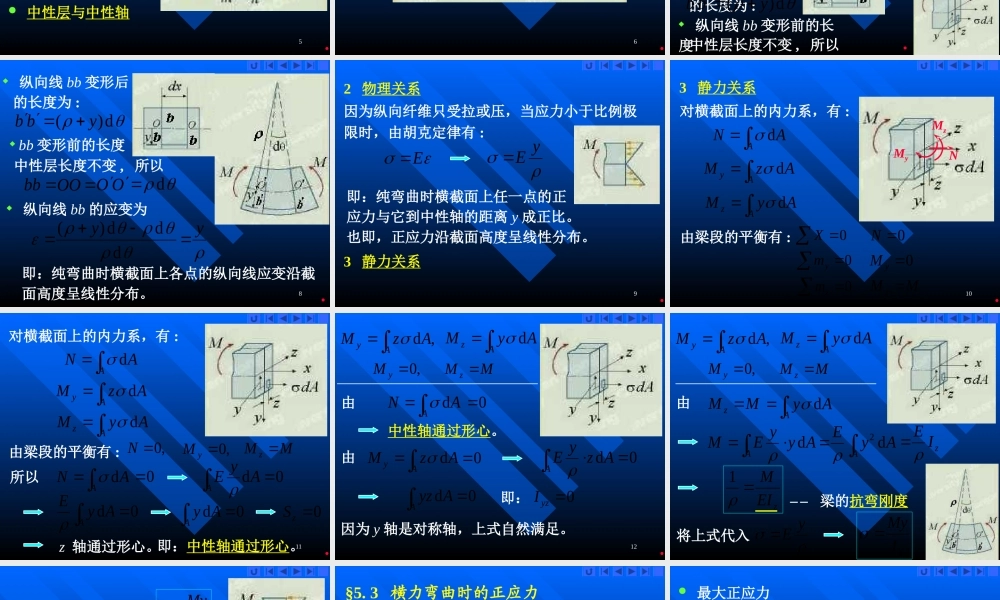
1材料力学材料力学2025年1月27日2025年1月27日星期一星期一第五章弯曲应力2第五章弯曲应力第五章弯曲应力本章内容:1纯弯曲2纯弯曲时的正应力3横力弯曲时的正应力4弯曲切应力5*关于弯曲理论的基本假设6提高弯曲强度的措施3§5.1纯弯曲横力弯曲梁的横截面上同时有弯矩和剪力的弯曲。纯弯曲梁的横截面上只有弯矩时的弯曲。横截面上只有正应力而无切应力。纯弯曲的变形特征4纯弯曲的变形特征5纯弯曲的变形特征基本假设1:平面假设变形前为平面的横截面变形后仍为平面，且仍垂直于梁的轴线。中性层与中性轴基本假设2:纵向纤维无挤压假设纵向纤维间无正应力。6中性层与中性轴7§5.2纯弯曲时的正应力1变形几何关系取坐标系如图，z轴为中性轴；y轴为对称轴。纵向线bb变形后的长度为:d)(ybb纵向线bb变形前的长度为求出距中性层y处的应变，取长dx的梁段研究:中性层长度不变,所以8纵向线bb变形后的长度为:d)(ybbbb变形前的长度bbOOOOd纵向线bb的应变为ddd)(yy即：纯弯曲时横截面上各点的纵向线应变沿截面高度呈线性分布。中性层长度不变,所以92物理关系因为纵向纤维只受拉或压，当应力小于比例极限时，由胡克定律有:EyE即：纯弯曲时横截面上任一点的正应力与它到中性轴的距离y成正比。也即，正应力沿截面高度呈线性分布。3静力关系10NMz3静力关系MyANAd0XAzMAydAyMAzd对横截面上的内力系，有:由梁段的平衡有:0N0ym0yM0zmMMz11ANAdAzMAydAyMAzd由梁段的平衡有:,0N,0yMMMz对横截面上的内力系，有:所以ANAd00dAyEA0dAyEA0dAyA0zSz轴通过形心。即：中性轴通过形心。12,dAzMAyAyMAzd,0yMMMz由ANAd00dAzyEA0dAyzA即：中性轴通过形心。由AzMAyd0因为y轴是对称轴，上式自然满足。0yzI13,dAzMAyAyMAzd,0yMMMz由梁的抗弯刚度MMzAyAdAyyEMAdAyEAd2zIEzEIM1将上式代入yEzIMy14由于推导过程并未用到矩形截面条件，因而公式适用于任何横截面具有纵向对称面，且载荷作用在对称面内的情况。公式是对等直梁得到的。对缓慢变化的变截面梁和曲率很小的曲梁也近似成立。公式是从纯弯曲梁推得是否适用于般纯弯曲时正应力公式zIMy公式的适用性15§5.3横力弯...