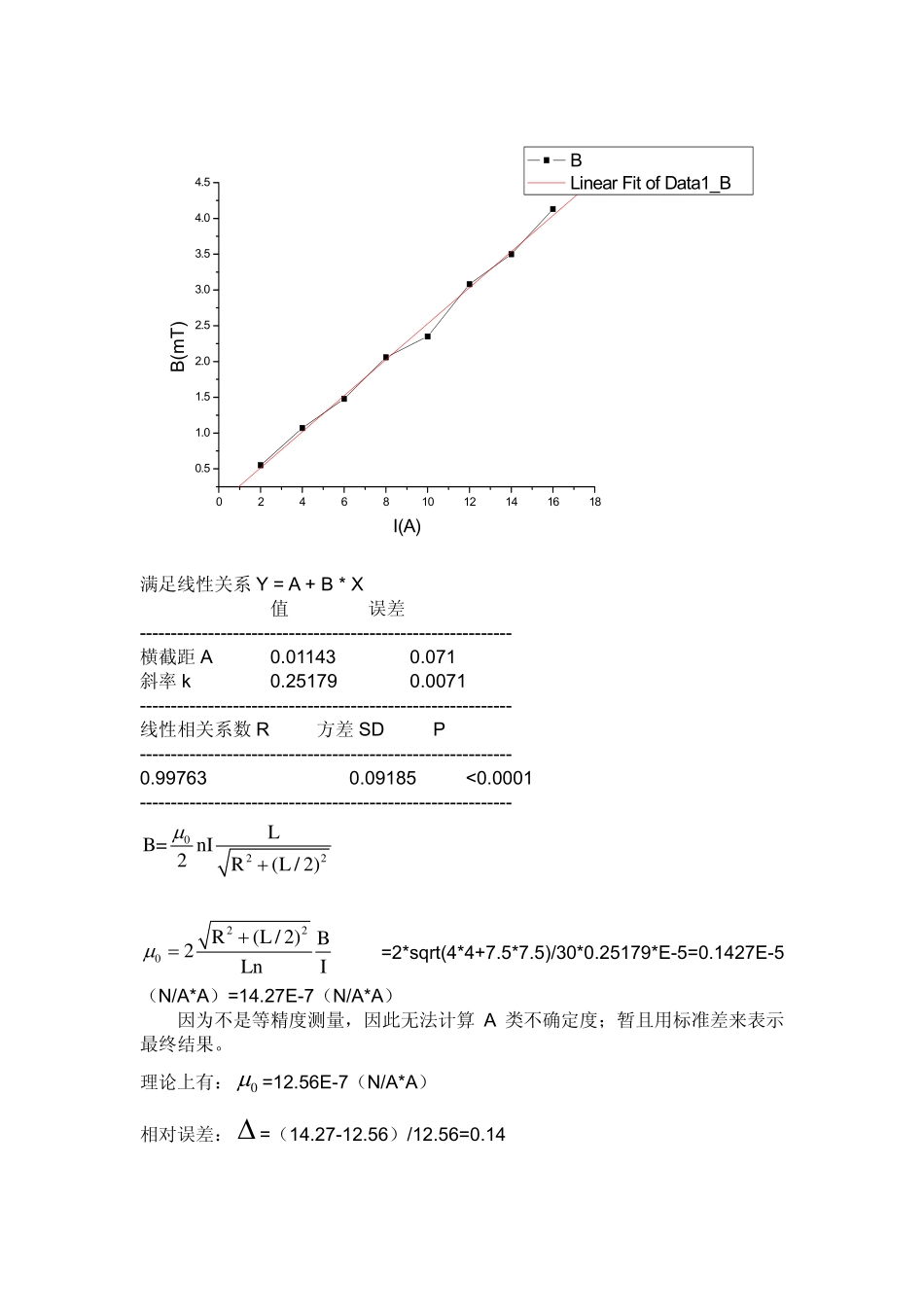
螺线管内的磁场系别:11姓名:孙翀学号:PB04210264一、实验目的:1、测量通电螺线管内的磁感应强度,讨论通电螺线管内部I,L,x和B之间的关系。2、计算出真空中的磁导率。二、实验设备:1、线管线圈;2、大电流电源;3、磁场强度计;4、探针。三、实验原理:0222xL/2x-L/2B=nI()2R(xL/2)R(x-L/2)2μ+−+++(L:螺线管长;x:螺线管中点到P的距离;n:单位长度的匝数)四、数据处理:1、L=15cm,x=0,N=30,R=4cm时B随I的变化:I(A)246810121416B(mT)0.551.071.482.062.353.083.504.13B—I曲线:0246810121416180.51.01.52.02.53.03.54.04.5B(mT)I(A)BLinearFitofData1_B满足线性关系Y=A+B*X值误差------------------------------------------------------------横截距A0.011430.071斜率k0.251790.0071------------------------------------------------------------线性相关系数R方差SDP------------------------------------------------------------0.997630.09185<0.0001------------------------------------------------------------022LB=nI2R(L/2)μ+220R(L/2)B2LnIμ+==2*sqrt(4*4+7.5*7.5)/30*0.25179*E-5=0.1427E-5(N/A*A)=14.27E-7(N/A*A)因为不是等精度测量,因此无法计算A类不确定度;暂且用标准差来表示最终结果。理论上有:0μ=12.56E-7(N/A*A)相对误差:=(14.27-12.56)/12.56=0.14Δ斜率的标准差为:k21S(1)/(n-2)*R=−k=0.00709E-5(N/A*A)=0.71E-7(N/A*A)最终结果:0μ=(14.270.71)E-7(N/A*A)±2、I=10A,x=0,N=30,R=4cm时B随L的变化:L(cm)810152025303540B(mT)3.413.302.391.981.701.361.281.16因B与L是非线性关系,因此不易用最小二乘法进行线性拟合。022LB=nI2R(L/2)μ+220R(L/2)B2LnIμ+=L(cm)810152025303540B(mT)3.413.302.391.981.701.361.281.160μe-712.8614.0813.5414.2214.8714.0715.3115.77平均值标准差б----------------------------------------------14.340.34因为不是等精度测量,因此无法计算A类不确定度;暂且用标准差来表示最终结果。理论上有:0μ=12.56E-7(N/A*A)相对误差:=(14.34-12.56)/12.56=0.14Δ最终结果:0μ=(14.34±0.34)E-7(N/A*A)3、如果探针没有处在螺线管的轴心位置,对实验结果会有影响,在边缘最小的地方会与中心相差0.3mT左右。这与螺线管内磁场的理论计算是相符的。误差分析及实验总结:1、本实验最难把握的就是探针的使用,要确保磁感线垂直从探针面传入,探针位于螺线管轴心位置,且恰在螺线管中点,这些都易带来误差;2、仪器误差如直尺的误差,电流计的误差,特斯拉表的误差等,另外注意每次测量时,要将电流源打到0点,特斯拉表重新调0;3、经过这次和上次的实验,对各种仪器的使用都较熟练了,而且已经研究了直导线、圆导线、螺线管的磁场与电流、距离的关系,为今后的电磁学习打下了基础。