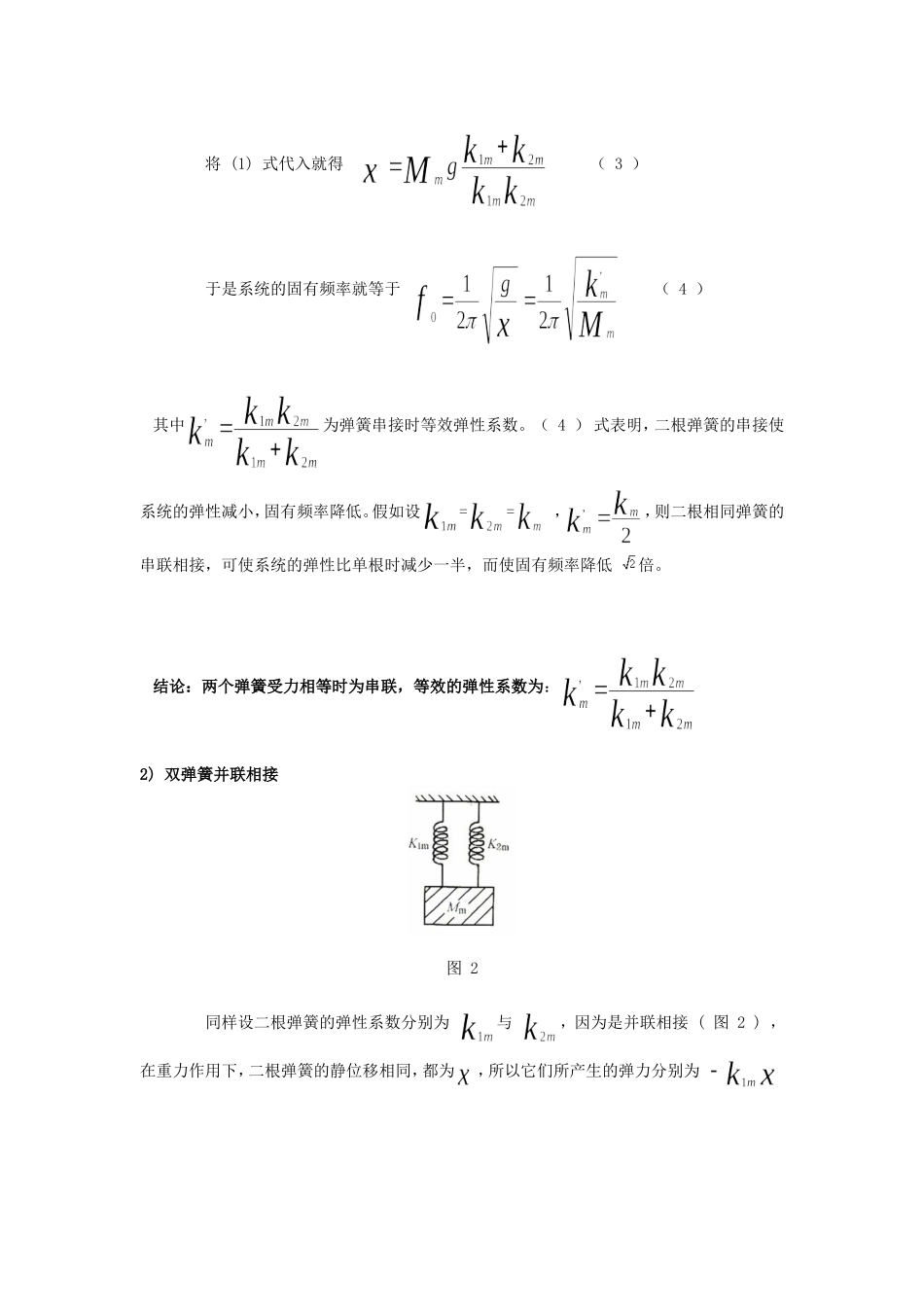
关于弹簧的一些简单讨论信院三班白潇pb05210258关键词:串联,并联,等效根据简谐振动的基础知识,弹簧的弹性力正比与弹簧的伸长量或缩短量,它满足胡克定律:。式中是物体相对平衡位置的位移,叫做弹性系数。越大,表示弹簧越硬。单个的弹簧模型在力学讨论中较为简单,而弹簧系统则较为复杂。我想在单个弹簧模型的基础上讨论弹簧的串,并联的等效变换的简单情况。一.下面我们分别来讨论双弹簧串联相接与并联相接的两种振动。1)双弹簧串联相接图1设二根弹簧的弹性系数分别为与。在质量的重力作用下,产生的静位移分别为与,如图1所示。于是每一弹簧所产生的弹力分别为与,因为二根弹簧是串联相接,每一根弹簧受到质量的拉力都相同,并且等于,因此根据静力学平衡条件可得2:(1)而二根弹簧的总静位移应等于各个弹簧静位移的总和,即(2)将(1)式代入就得(3)于是系统的固有频率就等于(4)其中为弹簧串接时等效弹性系数。(4)式表明,二根弹簧的串接使系统的弹性减小,固有频率降低。假如设==,,则二根相同弹簧的串联相接,可使系统的弹性比单根时减少一半,而使固有频率降低倍。结论:两个弹簧受力相等时为串联,等效的弹性系数为:2)双弹簧并联相接图2同样设二根弹簧的弹性系数分别为与,因为是并联相接(图2),在重力作用下,二根弹簧的静位移相同,都为,所以它们所产生的弹力分别为与。这时作用在质量上共有三个力,质量的重力和二根弹簧的弹力。根据静力学平衡条件可得(5)于是系统的固有频率就等于(6)其中为弹簧并接时等效弹性系数。(6)式表明,二根弹簧的并接使系统的弹性增大,固有频率提高。假如设,则二根相同的弹簧的并联相接,可使系统的弹性比单根时增加一倍,而使固有频率提高倍。结论:两个弹簧伸长量相等时为并联,等效的弹性系数为:二.再来讨论一般的情况有些系统的弹簧之间的关系不能简单的由串并联来描述,需要具体问题具体分析。要注意等效的条件是:1.等效弹簧应满足力等效2.等效弹簧应满足长度等效例:如图,求m上下振动的周期解:假设在c点有一与等效的弹簧(等长),故应满足:……(1)……(2),[1]陈克安《声学基础》西北工业大学航海学院环境工程系[2]杨维《力学》中国科学技术大学物理系